Bài 15 trang 103 Tài liệu dạy – học Toán 9 tập 2

Đề bài

Chứng minh \(\widehat {OAB} = \widehat {OBA} = \widehat {OCD} = \widehat {ODC} = \widehat {ODE} = \widehat {ODE} = \widehat {OEA} = \widehat {OAE}\)

Từ đó chứng minh nếu một ngũ giác nội tiếp và có các cạnh bằng nhau thì nó có phải là ngũ giác đều.

Lời giải chi tiết

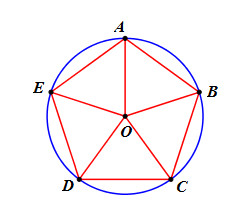
Ta có : \(AB = BC = CD = DE = EA \)

\(\Rightarrow cung\,AB = cung\,BC = cung\,CD = cung\,DE = cung\,EA\) (các dây bằng nhau căng các cung bằng nhau).

\( \Rightarrow \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA}\) (số đo góc ở tâm bằng số đo cung bị chắn).

Xét \(\Delta OAB\) có \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O.

\( \Rightarrow \widehat {OAB} = \widehat {OBA} = \dfrac{{{{180}^0} - \widehat {OAB}}}{2}\).

Chứng minh tương tự ta có

\(\begin{array}{l}\widehat {OBC} = \widehat {OCB} = \dfrac{{{{180}^0} - \widehat {BOC}}}{2}\\\widehat {OCD} = \widehat {ODC} = \dfrac{{{{180}^0} - \widehat {COD}}}{2}\\\widehat {ODE} = \widehat {ODE} = \dfrac{{{{180}^0} - \widehat {DOE}}}{2}\\\widehat {OEA} = \widehat {OAE} = \dfrac{{{{180}^0} - \widehat {EOA}}}{2}\end{array}\)

Mà \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA}\)

\(\begin{array}{l} \Rightarrow \widehat {OAB} = \widehat {OBA} = \widehat {OCD} = \widehat {ODC} = \widehat {ODE} = \widehat {ODE} = \widehat {OEA} = \widehat {OAE}\\ \Rightarrow \widehat {EAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA}\end{array}\)

Vậy ngũ giác ABCDE là ngũ giác đều (Ngũ giác có tất cả các cạnh bằng nhau và các góc bằng nhau).