Bài 11 trang 14 sách giáo khoa (SGK) Hình học 10 Nâng cao

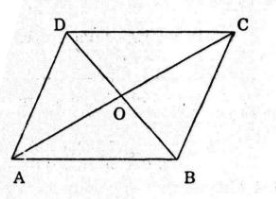
Cho hình bình hành \(ABCD\) với tâm \(O\). Mỗi khẳng định sau đây đúng hay sai ?

LG a

\(\left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = \left| {\overrightarrow {BD} } \right|\);

Giải chi tiết:

Sai vì \(\left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|\) thì chưa chắc \(AC, BD\) đã bằng nhau do \(ABCD\) là hình bình hành.

LG b

\(\overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {BC} \)

Giải chi tiết:

Đúng vì \(\overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {AD}  = \overrightarrow {BC} \)

LG c

\(\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OC}  + \overrightarrow {OD} \)

Giải chi tiết:

Sai vì \(\overrightarrow {OA}  + \overrightarrow {OB}  = \left( {\overrightarrow {OC}  + \overrightarrow {CA} } \right) + \left( {\overrightarrow {OD}  + \overrightarrow {DB} } \right) = \left( {\overrightarrow {OC}  + \overrightarrow {OD} } \right) + \left( {\overrightarrow {CA}  + \overrightarrow {DB} } \right) \ne \overrightarrow {OC}  + \overrightarrow {OD} \)

LG d

\(\overrightarrow {BD}  + \overrightarrow {AC}  = \overrightarrow {AD}  + \overrightarrow {BC} \).

Giải chi tiết:

Đúng vì \(\overrightarrow {BD}  + \overrightarrow {AC}  = \left( {\overrightarrow {BC}  + \overrightarrow {CD} } \right) + \left( {\overrightarrow {AD}  + \overrightarrow {DC} } \right) = \left( {\overrightarrow {DC}  + \overrightarrow {CD} } \right) + \left( {\overrightarrow {BC}  + \overrightarrow {AD} } \right) = \overrightarrow {AD}  + \overrightarrow {BC} \)