Bài 10 trang 71 SGK Toán 9 tập 2
Giải bài 10 trang 71 SGK Toán 9 tập 2. a) Vẽ đường tròn tâm O bán kinh R = 2 cm.
Đề bài
a) Vẽ đường tròn tâm \(O\) bán kính \(R = 2\) cm. Nêu cách vẽ cung \(\overparen{AB}\) có số đo bằng \(60^0\). Hỏi dây \(AB\) dài bao nhiêu xentimet?
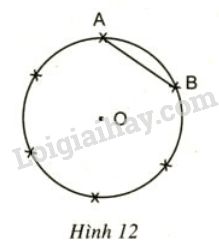
b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12.
Phương pháp giải - Xem chi tiết
a) Sử dụng số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó. Từ đó vẽ góc ở tâm bằng \(60^0\)
Sử dụng tính chất tam giác đều để suy ra độ dài dây \(AB\)
b) Sử dụng câu a) để vẽ 6 góc ở tâm bằng nhau và bằng \(60^0\), từ đó suy ra 6 cung bằng nhau.
Lời giải chi tiết
a) Vẽ đường tròn \((O; R)\). Vẽ góc ở tâm có số đo \(60^0\). Góc này là góc ở tâm chắn \(\overparen{AB}\) có số đo \(60^0\) (hình a).
Tam giác \(AOB\) cân có \(\widehat{O}=60^0\) nên AOB là tam giác đều, suy ra \(AB = R\).
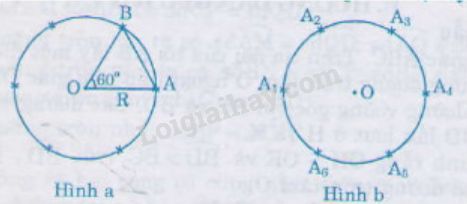
b) Theo câu a, ta có góc ở tâm bằng \(sđ\overparen{AB}=60^0\). Số đo góc ở tâm vẽ được theo cách này là \(360^0:60^0= 6\). Suy ra được \(6\) cung tròn bằng nhau trên đường tròn.
Từ đó suy ra cách vẽ như sau:
Vẽ \(6\) dây cung bằng nhau và bằng bán kính \(R\):
\(\overparen{{A_1}{A_2}} = \overparen{{A_2}{A_3}} = \overparen{{A_3}{A_4}}\)\(= \overparen{{A_4}{A_5}} = \overparen{{A_5}{A_6}} = \overparen{{A_6}{A_1}}\)
\(= {\rm{ }}R\)
Từ đó suy ra \(6\) cung bằng nhau. (hình b)
Hoặc ta có cách vẽ cụ thể như sau:
Chia đường tròn thành 6 cung bằng nhau:
+ Vẽ đường tròn tâm O, bán kính R.
+ Trên đường tròn tâm O, lấy điểm \(A_1\)
+ Vẽ cung tròn tâm \(A_1\), bán kính R cắt đường tròn tại \(A_2\) và \(A_6\)
+ Vẽ cung tròn tâm \(A_2\) và \(A_6\) bán kính R cắt đường tròn tâm O tại giao điểm thứ hai là \(A_3\) và \(A_5\)
+ Vẽ cung tròn tâm \(A_5\) bán kính R cắt đường tròn (O) tại giao điểm thứ hai là \(A_4\).
Khi đó, ta chia được đường tròn thành sáu cung bằng nhau như trên.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 10 trang 71 SGK Toán 9 tập 2 timdapan.com"







