Bài 1 trang 99 SGK Toán 9 tập 1
Giải bài 1 trang 99 SGK Toán 9 tập 1. Cho hình chữ nhật ABCD có AB=12cm, BC=5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn...
Đề bài
Cho hình chữ nhật \(ABCD\) có \(AB=12cm,\ BC=5cm\). Chứng minh rằng bốn điểm \(A,\ B,\ C,\ D\) thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Phương pháp giải - Xem chi tiết
+) Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm này cùng cách đều một điểm.
+) Sử dụng tính chất của hình chữ nhật: \(ABCD\) là hình chữ nhật, hai đường chéo cắt nhau tại \(O\) thì ta có \(OA=OB=OC=OD=\dfrac{AC}{2}=\dfrac{BD}{2}\).
+) Định lí Pytago: \(\Delta{ABC}\) vuông tại \(C\) thì \(BC^2=AB^2+AC^2.\)
Lời giải chi tiết
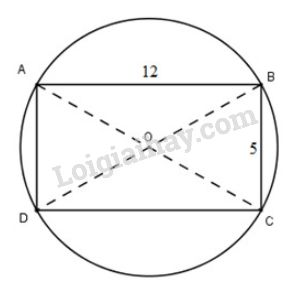
Gọi \(O\) là giao điểm hai đường chéo của hình chữ nhật, ta có \(OA = OB = OC = OD = R\).
Suy ra bốn điểm \(A,\ B,\ C,\ D\) cách đều điểm \(O\) nên bốn điểm này cùng thuộc đường tròn tâm \(O\).
Xét tam giác \(ABC\) vuông tại \(B\), áp dụng định lí Pytago, ta có:
\(AC^{2}=AB^{2}+BC^{2}=12^{2}+5^{2}=169\)
\(\Rightarrow AC=\sqrt{169}=13\,cm\)
Bán kính của đường tròn là: \(R=OB=OA=OC=OD=\dfrac{AC}{2}\)\(\,=\dfrac{13}{2}=6,5\,cm.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 99 SGK Toán 9 tập 1 timdapan.com"