Ôn tập chương 1 Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Video bài giảng
1. Kiến thức cần nhớ
- Sự đơn điệu của hàm số.
- Cực trị của hàm số.
- Giá trị lớn nhất - Giá trị nhỏ nhất của hàm số.
- Tiệm cận của đồ thị hàm số.
- Khảo sát sự biến thiên và vẽ đồ thị hàm số.
2. Một số dạng toán về sự đơn điệu của hàm số thường gặp
- Dạng 1: Xét tính đơn điệu của hàm số
- Dạng 2: Định giá trị của tham số m để hàm số đồng biến (nghịch biến) trên TXĐ.
3. Một số dạng toán về cực trị của hàm số thường gặp
- Dạng 1: Tìm các điểm cực trị của hàm số: Dùng quy tắc 1 hoặc quy tắc 2.
- Dạng 2: Định giá trị tham số m để hàm số đạt cực trị tại \(x_0.\)
Phương pháp:
- Tìm tập xác định.
- Tính \(y' \Rightarrow y'\left( {{x_0}} \right).\)
- Lập luận: Hàm số đạt cực đại tại \({x_0} \Rightarrow y'\left( {{x_0}} \right) = 0\), giải phương trình tìm được m.
- Với từng giá trị m vừa tìm được ta dùng quy tắc 1 hoặc quy tắc 2 kiểm tra lại xem có thỏa điều kiện đề bài không.
- Kết luận giá trị m thỏa điều kiện.
- Dạng 3: Định giá trị của tham số m để các hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,(a \ne 0)\) và
\(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\,\,(a,m \ne 0)\)cực đại, cực tiểu:
Phương pháp:
+ Tìm tập xác định D.
+ Tính \(y'\).
- Tính \(\Delta _{y'}\).
- Lập luận: Hàm số luôn luôn có CĐ, CT khi và chỉ khi phương trình \(y'=0\) có hai nghiệm phân biệt và đổi dấu hai lần khác nhau khi qua hai nghiệm đó. Phương trình \(y'=0\) có hai nghiệm phân biệt khi và chỉ khi \(\Delta _{y'}>0\) giải tìm m.
- Dạng 4: Định giá trị của tham số m để các hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,(a \ne 0)\) và
\(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\,\,(a,m \ne 0)\) không có cực đại, cực tiểu:
Phương pháp:
- Tìm tập xác định D.
- Tính \(y'\).
- Tính \(\Delta _{y'}\).
- Lập luận: Hàm số không có CĐ, CT khi và chỉ khi phương trình \(y'=0\) vô nghiệm hoặc có nghiệm kép. Phương trình \(y'=0\) có hai nghiệm phân biệt khi và chỉ khi \(\Delta _{y'}\leq 0\) giải tìm m.
- Dạng 5: Chứng minh với mọi giá trị của tham số m hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,(a \ne 0)\) luôn luôn có cực đại, cực tiểu.
Phương pháp:
- Tìm tập xác đinh D.
- Tính \(y'\).
- Tính \(\Delta _{y'}\) (nếu y’ là tam thức bậc 2 theo x).
- Chứng minh: \(\Delta _{y'}>0\) và y’ đổi dấu hai lần khác nhau khi qua hai nghiệm đó suy ra hàm số luôn luôn có cực đại, cực tiểu.
4. Giá trị lớn nhất - Giá trị nhỏ nhất của hàm số
- Tìm GTLN - GTNN của hàm sô trên một khoảng, nửa khoảng.
- Tìm GTLN - GTNN của hàm số trên một đoạn.
5. Khảo sát sự biến thiên và vẽ đồ thị hàm số
- Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba.
- Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn (trùng phương)
- Khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức bậc nhất/bậc nhất (hàm nhất biến).
6. Bài toán về sự tương giao của đồ thị hàm số
- Tìm số giao điểm của hai đường \((C_1):y=f(x)\) và \((C_2):y=g(x).\)
- Biện luận theo m nghiệm của phương trình \(f(x)=m.\)
7. Bài toán Về cực trị hàm số
Cho hàm số: \(y=\frac{1}{3}x^3-mx^2+(m^2-m+1)x+1\). Tìm m để hàm số:
a) Có cực đại và cực tiểu.
b) Đạt cực đại tại điểm x=1.
Lời giải:
TXĐ: \(D=\mathbb{R}.\)
Đạo hàm: \(y'=x^2-2mx+m^2-m+1\).
a) Tìm m để hàm số có cực đại và cực tiểu.
Hàm số có cực đại và cực tiểu khi và chỉ khi: y' = 0 có 2 nghiệm phân biệt.
Điều này xảy ra khi: \(\left\{ {\begin{array}{*{20}{c}}
{{a_{y'}} \ne 0}\\
{{{\Delta '}_{y'}} > 0}
\end{array}} \right.\)
\(\begin{array}{l}
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{1 \ne 0}\\
{{{( - m)}^2} - ({m^2} - m + 1) > 0}
\end{array}} \right.\\
\Leftrightarrow m - 1 > 0 \Leftrightarrow m > 1
\end{array}\)
b) Tìm m để hàm số đạt cực tiểu tại điểm x = 1
\(y'=x^2-2mx+m^2-m+1\) và
\(y''=2x-2m\)
Ta có:
\(\left\{\begin{matrix} y'(1)=0\\ y''(1)<0 \end{matrix}\right. \ \ \Leftrightarrow \left\{\begin{matrix} m^2-3m+2=0\\ 2-2m<0 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} m=1\vee m=2\\ m>1 \end{matrix}\right.\Leftrightarrow m=2\)
Thử lại với m = 2 hàm số đạt cực đại tại x = 1.
8. Bài toán Xác định m để hàm số nghịch biến
Định m để hàm số \(y=x^3+3x^2+(m+1)x+4m\) nghịch biến trên khoảng (-1;1).
Lời giải:
TXĐ: \(D=\mathbb{R}.\)
Đạo hàm: \(y'=3x^2+6x+m+1\)
Hàm số nghịch biến trên khoảng (-1;1) khi và chỉ khi \(y'\leq 0,\forall x\in (-1;1)\)
\(\Leftrightarrow 3x^2+6x+m+1\leq 0, \forall x\in (-1;1) \ \ (1)\)
Xét BPT (1) \(\Leftrightarrow m\leq -3x^2-6x-1=g(x)\)
Xét hàm số \(g(x), x\in (-1;1)\)
Có: \(g'(x)=-6x-6\leq 0, \forall x\in (-1;1)\)
BBT:
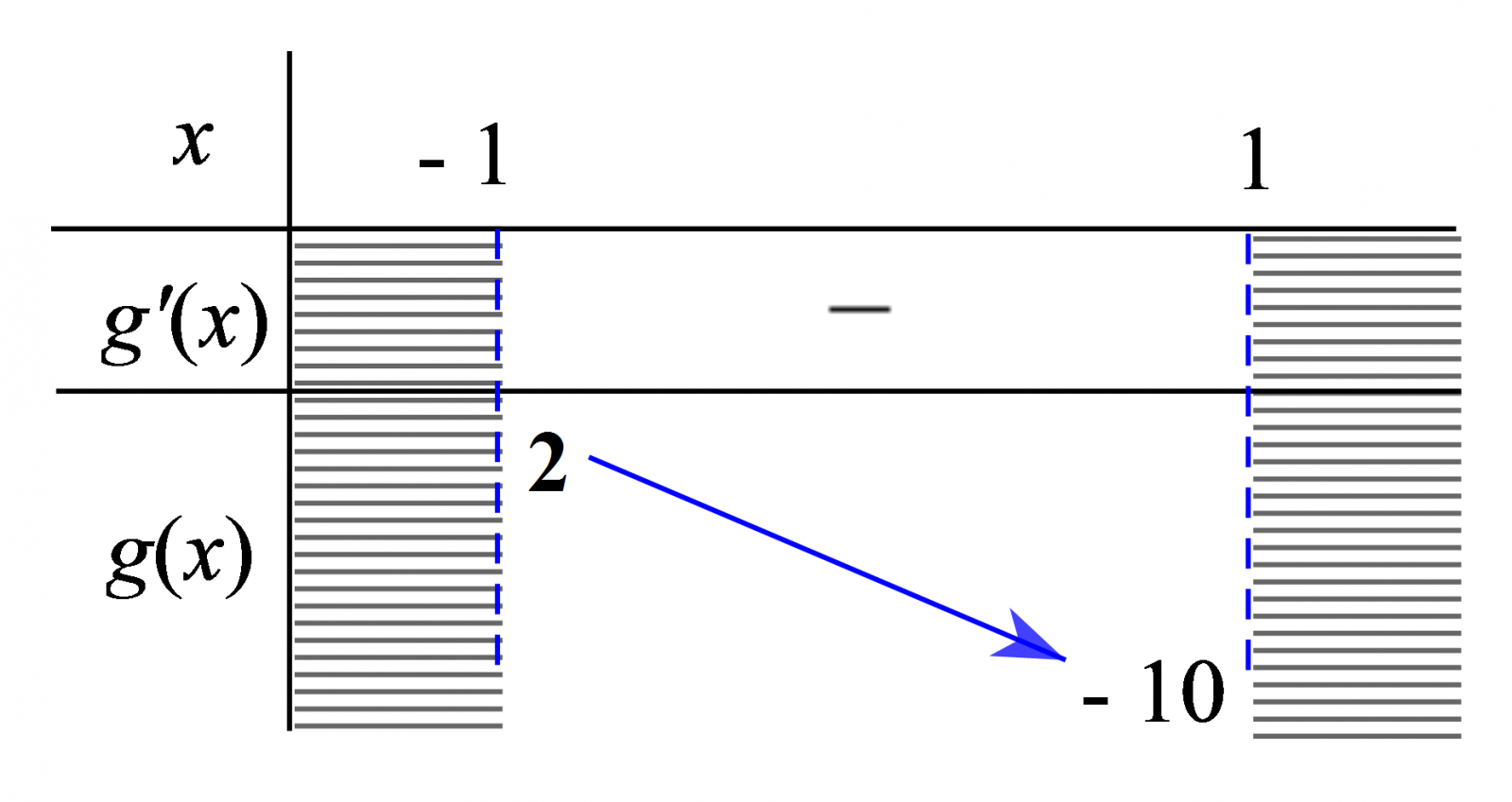
Từ BBT suy ra \(m\leq g(x), \forall x\in (-1;1)\Leftrightarrow m\leq -10\)
Vậy, hàm số nghịch biến trên khoảng \((-1;1)\) khi và chỉ khi \(m\leq 10.\)
9. Bài toán Tìm GTLN & GTNN
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x)=x^2-ln4x\) trên đoạn [1;e].
Lời giải:
\(f'(x)=2x-\frac{4}{x}=\frac{2x^2-4}{x}\); với \(x\in [1;e],f'(x)=0\Leftrightarrow x=\sqrt{2}\)
\(f(1)=1;f(e)=e^2-4;\)
Do đó:
\(\underset{x\in [1;e]}{min}f(x)=f(\sqrt{2})=2-2ln2\).
\(\underset{x\in [1;e]}{max}f(x)=f(e)=e^2-4\).
10. Bài toán Tìm m đề hàm số cắt trục hoành tại 4 điểm
Lời giải:
\(-x^4+(m+2)x^2-m-1=0\)
(C) cắt trục Ox tại 4 điểm phân biệt
\(\Leftrightarrow \left\{\begin{matrix} m+1>0\\ m+1\neq 1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-1\\ m\neq 0 \end{matrix}\right.\)
Khi đó:
Yêu cầu bài toán \(\Leftrightarrow \sqrt{m+1}<2\Leftrightarrow m+1<4\)
So với điều kiện (*) ta có giá trị cần tìm là: \(\left\{ \begin{array}{l}
- 1 < m < 3\\
m \ne 0
\end{array} \right.\)
1. Kiến thức cần nhớ
- Sự đơn điệu của hàm số.
- Cực trị của hàm số.
- Giá trị lớn nhất - Giá trị nhỏ nhất của hàm số.
- Tiệm cận của đồ thị hàm số.
- Khảo sát sự biến thiên và vẽ đồ thị hàm số.
2. Một số dạng toán về sự đơn điệu của hàm số thường gặp
- Dạng 1: Xét tính đơn điệu của hàm số
- Dạng 2: Định giá trị của tham số m để hàm số đồng biến (nghịch biến) trên TXĐ.
3. Một số dạng toán về cực trị của hàm số thường gặp
- Dạng 1: Tìm các điểm cực trị của hàm số: Dùng quy tắc 1 hoặc quy tắc 2.
- Dạng 2: Định giá trị tham số m để hàm số đạt cực trị tại \(x_0.\)
Phương pháp:
- Tìm tập xác định.
- Tính \(y' \Rightarrow y'\left( {{x_0}} \right).\)
- Lập luận: Hàm số đạt cực đại tại \({x_0} \Rightarrow y'\left( {{x_0}} \right) = 0\), giải phương trình tìm được m.
- Với từng giá trị m vừa tìm được ta dùng quy tắc 1 hoặc quy tắc 2 kiểm tra lại xem có thỏa điều kiện đề bài không.
- Kết luận giá trị m thỏa điều kiện.
- Dạng 3: Định giá trị của tham số m để các hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,(a \ne 0)\) và
\(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\,\,(a,m \ne 0)\)cực đại, cực tiểu:
Phương pháp:
+ Tìm tập xác định D.
+ Tính \(y'\).
- Tính \(\Delta _{y'}\).
- Lập luận: Hàm số luôn luôn có CĐ, CT khi và chỉ khi phương trình \(y'=0\) có hai nghiệm phân biệt và đổi dấu hai lần khác nhau khi qua hai nghiệm đó. Phương trình \(y'=0\) có hai nghiệm phân biệt khi và chỉ khi \(\Delta _{y'}>0\) giải tìm m.
- Dạng 4: Định giá trị của tham số m để các hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,(a \ne 0)\) và
\(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\,\,(a,m \ne 0)\) không có cực đại, cực tiểu:
Phương pháp:
- Tìm tập xác định D.
- Tính \(y'\).
- Tính \(\Delta _{y'}\).
- Lập luận: Hàm số không có CĐ, CT khi và chỉ khi phương trình \(y'=0\) vô nghiệm hoặc có nghiệm kép. Phương trình \(y'=0\) có hai nghiệm phân biệt khi và chỉ khi \(\Delta _{y'}\leq 0\) giải tìm m.
- Dạng 5: Chứng minh với mọi giá trị của tham số m hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,(a \ne 0)\) luôn luôn có cực đại, cực tiểu.
Phương pháp:
- Tìm tập xác đinh D.
- Tính \(y'\).
- Tính \(\Delta _{y'}\) (nếu y’ là tam thức bậc 2 theo x).
- Chứng minh: \(\Delta _{y'}>0\) và y’ đổi dấu hai lần khác nhau khi qua hai nghiệm đó suy ra hàm số luôn luôn có cực đại, cực tiểu.
4. Giá trị lớn nhất - Giá trị nhỏ nhất của hàm số
- Tìm GTLN - GTNN của hàm sô trên một khoảng, nửa khoảng.
- Tìm GTLN - GTNN của hàm số trên một đoạn.
5. Khảo sát sự biến thiên và vẽ đồ thị hàm số
- Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba.
- Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn (trùng phương)
- Khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức bậc nhất/bậc nhất (hàm nhất biến).
6. Bài toán về sự tương giao của đồ thị hàm số
- Tìm số giao điểm của hai đường \((C_1):y=f(x)\) và \((C_2):y=g(x).\)
- Biện luận theo m nghiệm của phương trình \(f(x)=m.\)
7. Bài toán Về cực trị hàm số
Cho hàm số: \(y=\frac{1}{3}x^3-mx^2+(m^2-m+1)x+1\). Tìm m để hàm số:
a) Có cực đại và cực tiểu.
b) Đạt cực đại tại điểm x=1.
Lời giải:
TXĐ: \(D=\mathbb{R}.\)
Đạo hàm: \(y'=x^2-2mx+m^2-m+1\).
a) Tìm m để hàm số có cực đại và cực tiểu.
Hàm số có cực đại và cực tiểu khi và chỉ khi: y' = 0 có 2 nghiệm phân biệt.
Điều này xảy ra khi: \(\left\{ {\begin{array}{*{20}{c}}
{{a_{y'}} \ne 0}\\
{{{\Delta '}_{y'}} > 0}
\end{array}} \right.\)
\(\begin{array}{l}
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{1 \ne 0}\\
{{{( - m)}^2} - ({m^2} - m + 1) > 0}
\end{array}} \right.\\
\Leftrightarrow m - 1 > 0 \Leftrightarrow m > 1
\end{array}\)
b) Tìm m để hàm số đạt cực tiểu tại điểm x = 1
\(y'=x^2-2mx+m^2-m+1\) và
\(y''=2x-2m\)
Ta có:
\(\left\{\begin{matrix} y'(1)=0\\ y''(1)<0 \end{matrix}\right. \ \ \Leftrightarrow \left\{\begin{matrix} m^2-3m+2=0\\ 2-2m<0 \end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} m=1\vee m=2\\ m>1 \end{matrix}\right.\Leftrightarrow m=2\)
Thử lại với m = 2 hàm số đạt cực đại tại x = 1.
8. Bài toán Xác định m để hàm số nghịch biến
Định m để hàm số \(y=x^3+3x^2+(m+1)x+4m\) nghịch biến trên khoảng (-1;1).
Lời giải:
TXĐ: \(D=\mathbb{R}.\)
Đạo hàm: \(y'=3x^2+6x+m+1\)
Hàm số nghịch biến trên khoảng (-1;1) khi và chỉ khi \(y'\leq 0,\forall x\in (-1;1)\)
\(\Leftrightarrow 3x^2+6x+m+1\leq 0, \forall x\in (-1;1) \ \ (1)\)
Xét BPT (1) \(\Leftrightarrow m\leq -3x^2-6x-1=g(x)\)
Xét hàm số \(g(x), x\in (-1;1)\)
Có: \(g'(x)=-6x-6\leq 0, \forall x\in (-1;1)\)
BBT:

Từ BBT suy ra \(m\leq g(x), \forall x\in (-1;1)\Leftrightarrow m\leq -10\)
Vậy, hàm số nghịch biến trên khoảng \((-1;1)\) khi và chỉ khi \(m\leq 10.\)
9. Bài toán Tìm GTLN & GTNN
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x)=x^2-ln4x\) trên đoạn [1;e].
Lời giải:
\(f'(x)=2x-\frac{4}{x}=\frac{2x^2-4}{x}\); với \(x\in [1;e],f'(x)=0\Leftrightarrow x=\sqrt{2}\)
\(f(1)=1;f(e)=e^2-4;\)
Do đó:
\(\underset{x\in [1;e]}{min}f(x)=f(\sqrt{2})=2-2ln2\).
\(\underset{x\in [1;e]}{max}f(x)=f(e)=e^2-4\).
10. Bài toán Tìm m đề hàm số cắt trục hoành tại 4 điểm
Lời giải:
\(-x^4+(m+2)x^2-m-1=0\)
(C) cắt trục Ox tại 4 điểm phân biệt
\(\Leftrightarrow \left\{\begin{matrix} m+1>0\\ m+1\neq 1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-1\\ m\neq 0 \end{matrix}\right.\)
Khi đó:
Yêu cầu bài toán \(\Leftrightarrow \sqrt{m+1}<2\Leftrightarrow m+1<4\)
So với điều kiện (*) ta có giá trị cần tìm là: \(\left\{ \begin{array}{l}
- 1 < m < 3\\
m \ne 0
\end{array} \right.\)