Bài 1: Sự đồng biến, nghịch biến của hàm số
Video bài giảng
1. Định nghĩa
Kí hiệu: K là một khoảng, một đoạn hoặc một nửa khoảng.
Cho hàm số \(y=f(x)\) xác định trên K.
- Hàm số \(y=f(x)\) đồng biến (tăng) trên K nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) < f({x_2})\).
- Hàm số \(y=f(x)\) nghịch biến (giảm) trên K nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) > f({x_2})\).
2. Điều kiện cần để hàm số đơn điệu
Cho hàm số \(y=f(x)\) có đạo hàm trên K:
- Nếu \(f(x)\) đồng biến trên K thì \(f'(x)\geq 0\) với mọi \(x\in K\).
- Nếu \(f(x)\) nghịch biến trên K thì \(f'(x)\leq 0\) với mọi \(x\in K\).
3. Điều kiện đủ để hàm số đơn điệu
Cho hàm số \(y=f(x)\) có đạo hàm trên K:
- Nếu \(f'(x)\geq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc K thì \(f(x)\) đồng biến trên K.
- Nếu \(f'(x)\leq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc K thì \(f(x)\) nghịch biến trên K.
- Nếu \(f'(x)=0\) với mọi \(x\in K\) thì \(f(x)\) là hàm hằng trên K.
4. Các bước xét tính đơn điệu của hàm số
- Bước 1: Tìm tập xác định
- Bước 2: Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
5. Bài toán Tìm khoảng đơn điệu của hàm số
Tìm khoảng đơn điệu của các hàm số sau:
a) \(y = {x^3} - 3{x^2} + 3x + 7\)
b) \(y=x^4-2x^2-1\)
c) \(y=\frac{x+1}{x-1}\)
Lời giải:
a) \(y = {x^3} - 3{x^2} + 3x + 7\)
Xét hàm số: \(y = {x^3} - 3{x^2} + 3x + 7\)
TXĐ: \(D=\mathbb{R}\)
\(y'=3x^2-6x+3\)
\(y' = 0 \Leftrightarrow 3{x^2} - 6x + 3 = 0 \Leftrightarrow x = 1\)
Bảng biến thiên:

Kết luận: Hàm số đồng biến trên \(\mathbb{R}.\)
b) \(y=x^4-2x^2-1\)
Xét hàm số \(y=x^4-2x^2-1\)
TXĐ: \(D=\mathbb{R}\)
\(y'=4x^3-4x\)
\(y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = - 1\\ x = 1 \end{array} \right.\)
Bảng biến thiên:
.png)
Kết luận:
- Hàm số đồng biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\)
- Hàm số nghịch biến trên các khoảng \(\left( {- \infty;-1 } \right)\) và \((0;1).\)
c) \(y=\frac{x+1}{x-1}\)
Xét hàm số \(y=\frac{x+1}{x-1}\).
TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
\(y' = \frac{{ - 2}}{{{{(x - 1)}^2}}} > 0,\forall \ne 1\)
Bảng biến thiên:
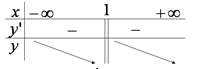
Kết luận: Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( { 1;+ \infty } \right)\).
6. Bài toán Tìm tham số để hàm số đơn điệu trên một miền
Ví dụ 1:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=x^3+3x^2+mx+m\) đồng biến trên \(\mathbb{R}\).
Lời giải:
Xét hàm số \(y=x^3+3x^2+mx+m\)
TXĐ: \(D=\mathbb{R}\)
\(y' = 3{x^2} + 6x + m\)
Hàm số đồng biến trên \(\mathbb{R}\) khi \(y' \ge 0,\forall x \in\mathbb{R} \Leftrightarrow \left\{ \begin{array}{l} \Delta ' \le 0\\ a = 1 > 0 \end{array} \right. \Leftrightarrow 9 - 3m < 0 \Leftrightarrow m \ge 3\).
Kết luận: với \(m\geq 3\) thì hàm số đồng biến trên \(\mathbb{R}\).
Ví dụ 2:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y = 2x^3 - 3(2m + 1){x^2} + 6m(m + 1)x + 1\) đồng biến trong khoảng \((2; + \infty )\).
Lời giải:
Xét hàm số \(y = 2x^3 - 3(2m + 1){x^2} + 6m(m + 1)x + 1\).
TXĐ: \(D=\mathbb{R}\)
\(y' = 6{x^2} - 6(2m + 1)x + 6m(m + 1)\)
\(\Delta = {(2m + 1)^2} - 4({m^2} + m) = 1 > 0\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = m\\ x = m + 1 \end{array} \right.\)
.png)
Hàm số đồng biến trong các khoảng \(( - \infty ;m),\,\,(m + 1; + \infty )\).
Kết luận: Do đó hàm số đồng biến trong khoảng \((2; + \infty )\) khi \(m + 1 \le 2 \Leftrightarrow m \le 1.\)
1. Định nghĩa
Kí hiệu: K là một khoảng, một đoạn hoặc một nửa khoảng.
Cho hàm số \(y=f(x)\) xác định trên K.
- Hàm số \(y=f(x)\) đồng biến (tăng) trên K nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) < f({x_2})\).
- Hàm số \(y=f(x)\) nghịch biến (giảm) trên K nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) > f({x_2})\).
2. Điều kiện cần để hàm số đơn điệu
Cho hàm số \(y=f(x)\) có đạo hàm trên K:
- Nếu \(f(x)\) đồng biến trên K thì \(f'(x)\geq 0\) với mọi \(x\in K\).
- Nếu \(f(x)\) nghịch biến trên K thì \(f'(x)\leq 0\) với mọi \(x\in K\).
3. Điều kiện đủ để hàm số đơn điệu
Cho hàm số \(y=f(x)\) có đạo hàm trên K:
- Nếu \(f'(x)\geq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc K thì \(f(x)\) đồng biến trên K.
- Nếu \(f'(x)\leq 0\) với mọi \(x\in K\) và \(f'(x)=0\) chỉ tại một số hữu hạn điểm thuộc K thì \(f(x)\) nghịch biến trên K.
- Nếu \(f'(x)=0\) với mọi \(x\in K\) thì \(f(x)\) là hàm hằng trên K.
4. Các bước xét tính đơn điệu của hàm số
- Bước 1: Tìm tập xác định
- Bước 2: Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
5. Bài toán Tìm khoảng đơn điệu của hàm số
Tìm khoảng đơn điệu của các hàm số sau:
a) \(y = {x^3} - 3{x^2} + 3x + 7\)
b) \(y=x^4-2x^2-1\)
c) \(y=\frac{x+1}{x-1}\)
Lời giải:
a) \(y = {x^3} - 3{x^2} + 3x + 7\)
Xét hàm số: \(y = {x^3} - 3{x^2} + 3x + 7\)
TXĐ: \(D=\mathbb{R}\)
\(y'=3x^2-6x+3\)
\(y' = 0 \Leftrightarrow 3{x^2} - 6x + 3 = 0 \Leftrightarrow x = 1\)
Bảng biến thiên:

Kết luận: Hàm số đồng biến trên \(\mathbb{R}.\)
b) \(y=x^4-2x^2-1\)
Xét hàm số \(y=x^4-2x^2-1\)
TXĐ: \(D=\mathbb{R}\)
\(y'=4x^3-4x\)
\(y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = - 1\\ x = 1 \end{array} \right.\)
Bảng biến thiên:
.png)
Kết luận:
- Hàm số đồng biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\)
- Hàm số nghịch biến trên các khoảng \(\left( {- \infty;-1 } \right)\) và \((0;1).\)
c) \(y=\frac{x+1}{x-1}\)
Xét hàm số \(y=\frac{x+1}{x-1}\).
TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
\(y' = \frac{{ - 2}}{{{{(x - 1)}^2}}} > 0,\forall \ne 1\)
Bảng biến thiên:

Kết luận: Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( { 1;+ \infty } \right)\).
6. Bài toán Tìm tham số để hàm số đơn điệu trên một miền
Ví dụ 1:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=x^3+3x^2+mx+m\) đồng biến trên \(\mathbb{R}\).
Lời giải:
Xét hàm số \(y=x^3+3x^2+mx+m\)
TXĐ: \(D=\mathbb{R}\)
\(y' = 3{x^2} + 6x + m\)
Hàm số đồng biến trên \(\mathbb{R}\) khi \(y' \ge 0,\forall x \in\mathbb{R} \Leftrightarrow \left\{ \begin{array}{l} \Delta ' \le 0\\ a = 1 > 0 \end{array} \right. \Leftrightarrow 9 - 3m < 0 \Leftrightarrow m \ge 3\).
Kết luận: với \(m\geq 3\) thì hàm số đồng biến trên \(\mathbb{R}\).
Ví dụ 2:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y = 2x^3 - 3(2m + 1){x^2} + 6m(m + 1)x + 1\) đồng biến trong khoảng \((2; + \infty )\).
Lời giải:
Xét hàm số \(y = 2x^3 - 3(2m + 1){x^2} + 6m(m + 1)x + 1\).
TXĐ: \(D=\mathbb{R}\)
\(y' = 6{x^2} - 6(2m + 1)x + 6m(m + 1)\)
\(\Delta = {(2m + 1)^2} - 4({m^2} + m) = 1 > 0\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = m\\ x = m + 1 \end{array} \right.\)
.png)
Hàm số đồng biến trong các khoảng \(( - \infty ;m),\,\,(m + 1; + \infty )\).
Kết luận: Do đó hàm số đồng biến trong khoảng \((2; + \infty )\) khi \(m + 1 \le 2 \Leftrightarrow m \le 1.\)