Bài 2: Cực trị của hàm số
Video bài giảng
1. Định nghĩa
Cho hàm số \(y=f(x)\) liên tục trên khoảng (a;b) và điểm \(x_0\in(a;b)\):
- Hàm số \(f(x)\) đạt cực đại tại \(x_0\) nếu
\(f(x_0)>f(x)\)
\(\forall x\in (x_0-h,x_0+h) \setminus \left \{ x_0 \right \},h>0\)
- Hàm số \(f(x)\) đạt cực tiểu tại \(x_0\) nếu
\(f({x_0}) < f(x)\)
\(\forall x \in ({x_0} - h,{x_0} + h)\backslash \left\{ {{x_0}} \right\},h > 0\)
2. Điều kiện cần và điều kiện đủ để hàm số có cực trị
a) Điều kiện cần để hàm số có cực trị
\(f(x)\) đạt cực trị tại \(x_0\), có đạo hàm tại \(x_0\) thì \(f'(x_0)=0\).
b) Điều kiện đủ để hàm số có điểm cực đại và cực tiểu
Điều kiện thứ nhất: Cho hàm số \(y=f(x)\) liên tục trên khoảng
\(K = ({x_0} - h;{x_0} + h)\,(h > 0)\) và có đạo hàm trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\):
- Nếu \(\left\{ \begin{array}{l}
f'\left( x \right) < 0,\forall x \in \left( {{x_0} - h;{x_0}} \right)\\
f'\left( x \right) > 0,\forall x \in \left( {{x_0};{x_0} + h} \right)
\end{array} \right.\)
thì x0 là điểm cực tiểu của hàm số \(f(x)\).
- Nếu \(\left\{ \begin{array}{l}
f'\left( x \right) > 0,\forall x \in \left( {{x_0} - h;{x_0}} \right)\\
f'\left( x \right) < 0,\forall x \in \left( {{x_0};{x_0} + h} \right)
\end{array} \right.\)
thì x0 là điểm cực đại của hàm số \(f(x)\).
Cách phát biểu khác dễ hiểu hơn: Đi từ trái sang phải
- Nếu \(f(x)\) đổi dấu từ - sang + khi qua \(x_0\) thì \(x_0\) là điểm cực tiểu.
- Nếu \(f(x)\) đổi dấu từ + sang - khi qua \(x_0\) thì \(x_0\) là điểm cực đại.
Điều kiện thứ hai: Cho hàm số \(y=f(x)\) có đạo hàm cấp hai trên khoảng \(K = ({x_0} - h;{x_0} + h)\,(h > 0)\):
- Nếu \(f'(x_0)=0\), \(f''(x_0)<0\) thì \(x_0\) là điểm cực đại của hàm số \(f(x)\).
- Nếu \(f'(x_0)=0\), \(f''(x_0)>0\) thì \(x_0\) là điểm cực tiểu của hàm số \(f(x)\).
3. Qui tắc tìm cực trị
a) Quy tắc 1
- Tìm tập xác định.
- Tính \(f'(x)\). Tìm các điểm tại đó\(f'(x)=0\) hoặc \(f'(x)\) không xác định.
- Lập bảng biến thiên.
- Từ bảng biến thiên suy ra các điểm cực đại, cực tiểu.
b) Quy tắc 2
- Tìm tập xác định.
- Tính \(f'(x)\). Tìm các nghiệm
của phương trình \(f'(x)=0\).
- Tính \(f''(x)\) và \(f''(x_i)\) suy ra tính chất cực trị của các điểm \({x_i}\).
Chú ý: Nếu \(f''(x_i)=0\) thì ta phải dùng quy tắc 1 để xét cực trị tại \({x_i}\).
4. Bài toán Tìm cực trị của hàm số
Ví dụ 1:
Tìm các điểm cực đại, cực tiểu của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - {x^2} - 3x + \frac{4}{3}\)
b) \(y = \left| x \right|\left( {x + 2} \right)\)
Lời giải:
a) \(y = \frac{1}{3}{x^3} - {x^2} - 3x + \frac{4}{3}\)
Cách 1:
Hàm số có TXĐ: \(D=\mathbb{R}\)
\(y' = {x^2} - 2x - 3\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 3 \end{array} \right.\)
Bảng biến thiên:
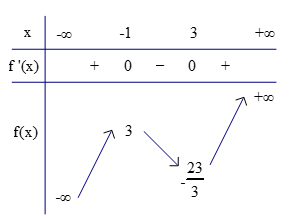
Kết luận:
- Hàm số đạt cực đại tại \(x=-1\), giá trị cực đại tương ứng là \(y(-1)=3\);
- Hàm số đạt cực tiểu tại \(x=3\), giá trị cực tiểu tương ứng là \(y_{CD}=-\frac{23}{3}\).
Cách 2:
Hàm số có TXĐ: \(D=\mathbb{R}\)
\(y' = {x^2} - 2x - 3\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 3 \end{array} \right.\)
\(y ''= 2x - 2\)
- \(y''\left( { - 1} \right) = - 4 < 0\) suy ra hàm số đạt cực đại tại \(x=-1\), giá trị cực đại tương ứng là \(y(-1)=3\).
- \(y''\left( 3 \right) = 4 > 0\) suy ra hàm số đạt cực tiểu tại \(x=3\), giá trị cực tiểu tương ứng là \(y_{CD}=-\frac{23}{3}\).
b) \(y = \left| x \right|\left( {x + 2} \right)\)
Hàm số có TXĐ: \(D=\mathbb{R}\)
\(y' = \frac{x}{{\left| x \right|}}\left( {x + 2} \right) + \left| x \right| = \frac{{2\left( {{x^2} + x} \right)}}{{\left| x \right|}} (x\ne0)\)
Bảng biến thiên:

Kết luận:
- Hàm số đạt cực đại tại \(x=-1,\) giá trị cực đại tương ứng là \(y(-1)=1;\)
- Hàm số đạt cực tiểu tại \(x=0,\) giá trị cực tiểu \(y(0)=0.\)
Ví dụ 2:
Tìm các điểm cực đại, cực tiểu của hàm số \(y=x-sin2x+2.\)
Lời giải:
Hàm số có TXĐ: \(D=\mathbb{R}\)
\(y' = 1 - 2\cos 2x\)
\(y'=0 \Leftrightarrow \cos2x\Leftrightarrow x = \pm \frac{\pi }{6} + k\pi (k\in\mathbb{Z})\)
\(y'' = 4\sin 2x\)
- \(y''\left( {\frac{\pi }{6} + k\pi } \right) = 4\sin \left( {\frac{\pi }{3} + 2k\pi } \right) \)
\(= 2\sqrt 3 > 0\) suy ra hàm số đạt cực tiểu tại \(x = \frac{\pi }{6} + k\pi\), giá trị cực tiểu tương ứng là \(y\left( {\frac{\pi }{6} + k\pi } \right) = {\textstyle{\pi \over 6}} + k\pi - \frac{{\sqrt 3 }}{2} + 2\).
- \(y''\left( { - \frac{\pi }{6} + k\pi } \right) = 4\sin \left( { - \frac{\pi }{3} + 2k\pi } \right) \)
\(= - 2\sqrt 3 < 0\) suy ra hàm số đạt cực đại tại \(x = -\frac{\pi }{6} + k\pi\), giá trị cực đại tương ứng là \(y\left( { - \frac{\pi }{6} + k\pi } \right) = - \frac{\pi }{6} + k\pi - \frac{{\sqrt 3 }}{2} + 2\).
5. Bài toán Tìm tham số để hàm số có cực trị thỏa mãn điều kiện cho trước
Ví dụ 1:
Tìm m để hàm số \(y = \left( {m + 2} \right){x^3} + 3{x^2} + mx - 5\) có 2 cực trị
Lời giải:
+ Với m = -2 hàm số trở thành
\(y = 3{x^2} - 2x - 5\) không thể có hai cực trị. (1)
+ Với \(m\ne-2\) ta có:
\(y' = 3\left( {m + 2} \right){x^2} + 6x + m\)
- Hàm số có hai cực trị khi và chỉ khi phương trình \(y'=0\) có hai nghiệm phân biệt.
- Điều này xảy ra khi:
\(\Delta ' = - 3\left( {{m^2} + 2m - 3} \right) > 0 \)
\(\Leftrightarrow {m^2} + 2m - 3 < 0 \Leftrightarrow - 3 < m < 1.\) (2)
+ Từ (1) (2) suy ra hàm số có hai cực trị khi: \(m \in \left( { - 3; - 2} \right) \cup \left( { - 2;1} \right)\)
Ví dụ 2:
Tìm tất cả các giá trị thực của tham số m để hàm số
\(\: y = -x^3 + (m+3)x^2 - (m^2 + 2m)x - 2\) đạt cực đại tại \(x=2.\)
Lời giải:
Hàm số có tập xác định: \(D=\mathbb{R}\).
\(y' = -3x^2 + 2(m+3)x-(m^2 + 2m);\)
Để hàm số có cực trị tại \(x=2\) thì:
\(y'(2) = 0 \)
\(\Leftrightarrow - 12 + 4(m + 3) - {m^2} - 2m = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l} m = 0\\ m = 2 \end{array} \right.\)
Ta có: \(y'' = - 6x + 2(m + 3)\)
+ Với \(m=0\) thì \(y''(2)=-6<0.\)
+ Với \(m=2\) thì \(y''(2)=-2<0\).
Thứ lại với \(m=0\) và \(m=2\) hàm số đều đạt cực đại tại x = 2.
1. Định nghĩa
Cho hàm số \(y=f(x)\) liên tục trên khoảng (a;b) và điểm \(x_0\in(a;b)\):
- Hàm số \(f(x)\) đạt cực đại tại \(x_0\) nếu
\(f(x_0)>f(x)\)
\(\forall x\in (x_0-h,x_0+h) \setminus \left \{ x_0 \right \},h>0\)
- Hàm số \(f(x)\) đạt cực tiểu tại \(x_0\) nếu
\(f({x_0}) < f(x)\)
\(\forall x \in ({x_0} - h,{x_0} + h)\backslash \left\{ {{x_0}} \right\},h > 0\)
2. Điều kiện cần và điều kiện đủ để hàm số có cực trị
a) Điều kiện cần để hàm số có cực trị
\(f(x)\) đạt cực trị tại \(x_0\), có đạo hàm tại \(x_0\) thì \(f'(x_0)=0\).
b) Điều kiện đủ để hàm số có điểm cực đại và cực tiểu
Điều kiện thứ nhất: Cho hàm số \(y=f(x)\) liên tục trên khoảng
\(K = ({x_0} - h;{x_0} + h)\,(h > 0)\) và có đạo hàm trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\):
- Nếu \(\left\{ \begin{array}{l}
f'\left( x \right) < 0,\forall x \in \left( {{x_0} - h;{x_0}} \right)\\
f'\left( x \right) > 0,\forall x \in \left( {{x_0};{x_0} + h} \right)
\end{array} \right.\)
thì x0 là điểm cực tiểu của hàm số \(f(x)\).
- Nếu \(\left\{ \begin{array}{l}
f'\left( x \right) > 0,\forall x \in \left( {{x_0} - h;{x_0}} \right)\\
f'\left( x \right) < 0,\forall x \in \left( {{x_0};{x_0} + h} \right)
\end{array} \right.\)
thì x0 là điểm cực đại của hàm số \(f(x)\).
Cách phát biểu khác dễ hiểu hơn: Đi từ trái sang phải
- Nếu \(f(x)\) đổi dấu từ - sang + khi qua \(x_0\) thì \(x_0\) là điểm cực tiểu.
- Nếu \(f(x)\) đổi dấu từ + sang - khi qua \(x_0\) thì \(x_0\) là điểm cực đại.
Điều kiện thứ hai: Cho hàm số \(y=f(x)\) có đạo hàm cấp hai trên khoảng \(K = ({x_0} - h;{x_0} + h)\,(h > 0)\):
- Nếu \(f'(x_0)=0\), \(f''(x_0)<0\) thì \(x_0\) là điểm cực đại của hàm số \(f(x)\).
- Nếu \(f'(x_0)=0\), \(f''(x_0)>0\) thì \(x_0\) là điểm cực tiểu của hàm số \(f(x)\).
3. Qui tắc tìm cực trị
a) Quy tắc 1
- Tìm tập xác định.
- Tính \(f'(x)\). Tìm các điểm tại đó\(f'(x)=0\) hoặc \(f'(x)\) không xác định.
- Lập bảng biến thiên.
- Từ bảng biến thiên suy ra các điểm cực đại, cực tiểu.
b) Quy tắc 2
- Tìm tập xác định.
- Tính \(f'(x)\). Tìm các nghiệm
của phương trình \(f'(x)=0\).
- Tính \(f''(x)\) và \(f''(x_i)\) suy ra tính chất cực trị của các điểm \({x_i}\).
Chú ý: Nếu \(f''(x_i)=0\) thì ta phải dùng quy tắc 1 để xét cực trị tại \({x_i}\).
4. Bài toán Tìm cực trị của hàm số
Ví dụ 1:
Tìm các điểm cực đại, cực tiểu của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - {x^2} - 3x + \frac{4}{3}\)
b) \(y = \left| x \right|\left( {x + 2} \right)\)
Lời giải:
a) \(y = \frac{1}{3}{x^3} - {x^2} - 3x + \frac{4}{3}\)
Cách 1:
Hàm số có TXĐ: \(D=\mathbb{R}\)
\(y' = {x^2} - 2x - 3\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 3 \end{array} \right.\)
Bảng biến thiên:

Kết luận:
- Hàm số đạt cực đại tại \(x=-1\), giá trị cực đại tương ứng là \(y(-1)=3\);
- Hàm số đạt cực tiểu tại \(x=3\), giá trị cực tiểu tương ứng là \(y_{CD}=-\frac{23}{3}\).
Cách 2:
Hàm số có TXĐ: \(D=\mathbb{R}\)
\(y' = {x^2} - 2x - 3\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = 3 \end{array} \right.\)
\(y ''= 2x - 2\)
- \(y''\left( { - 1} \right) = - 4 < 0\) suy ra hàm số đạt cực đại tại \(x=-1\), giá trị cực đại tương ứng là \(y(-1)=3\).
- \(y''\left( 3 \right) = 4 > 0\) suy ra hàm số đạt cực tiểu tại \(x=3\), giá trị cực tiểu tương ứng là \(y_{CD}=-\frac{23}{3}\).
b) \(y = \left| x \right|\left( {x + 2} \right)\)
Hàm số có TXĐ: \(D=\mathbb{R}\)
\(y' = \frac{x}{{\left| x \right|}}\left( {x + 2} \right) + \left| x \right| = \frac{{2\left( {{x^2} + x} \right)}}{{\left| x \right|}} (x\ne0)\)
Bảng biến thiên:

Kết luận:
- Hàm số đạt cực đại tại \(x=-1,\) giá trị cực đại tương ứng là \(y(-1)=1;\)
- Hàm số đạt cực tiểu tại \(x=0,\) giá trị cực tiểu \(y(0)=0.\)
Ví dụ 2:
Tìm các điểm cực đại, cực tiểu của hàm số \(y=x-sin2x+2.\)
Lời giải:
Hàm số có TXĐ: \(D=\mathbb{R}\)
\(y' = 1 - 2\cos 2x\)
\(y'=0 \Leftrightarrow \cos2x\Leftrightarrow x = \pm \frac{\pi }{6} + k\pi (k\in\mathbb{Z})\)
\(y'' = 4\sin 2x\)
- \(y''\left( {\frac{\pi }{6} + k\pi } \right) = 4\sin \left( {\frac{\pi }{3} + 2k\pi } \right) \)
\(= 2\sqrt 3 > 0\) suy ra hàm số đạt cực tiểu tại \(x = \frac{\pi }{6} + k\pi\), giá trị cực tiểu tương ứng là \(y\left( {\frac{\pi }{6} + k\pi } \right) = {\textstyle{\pi \over 6}} + k\pi - \frac{{\sqrt 3 }}{2} + 2\).
- \(y''\left( { - \frac{\pi }{6} + k\pi } \right) = 4\sin \left( { - \frac{\pi }{3} + 2k\pi } \right) \)
\(= - 2\sqrt 3 < 0\) suy ra hàm số đạt cực đại tại \(x = -\frac{\pi }{6} + k\pi\), giá trị cực đại tương ứng là \(y\left( { - \frac{\pi }{6} + k\pi } \right) = - \frac{\pi }{6} + k\pi - \frac{{\sqrt 3 }}{2} + 2\).
5. Bài toán Tìm tham số để hàm số có cực trị thỏa mãn điều kiện cho trước
Ví dụ 1:
Tìm m để hàm số \(y = \left( {m + 2} \right){x^3} + 3{x^2} + mx - 5\) có 2 cực trị
Lời giải:
+ Với m = -2 hàm số trở thành
\(y = 3{x^2} - 2x - 5\) không thể có hai cực trị. (1)
+ Với \(m\ne-2\) ta có:
\(y' = 3\left( {m + 2} \right){x^2} + 6x + m\)
- Hàm số có hai cực trị khi và chỉ khi phương trình \(y'=0\) có hai nghiệm phân biệt.
- Điều này xảy ra khi:
\(\Delta ' = - 3\left( {{m^2} + 2m - 3} \right) > 0 \)
\(\Leftrightarrow {m^2} + 2m - 3 < 0 \Leftrightarrow - 3 < m < 1.\) (2)
+ Từ (1) (2) suy ra hàm số có hai cực trị khi: \(m \in \left( { - 3; - 2} \right) \cup \left( { - 2;1} \right)\)
Ví dụ 2:
Tìm tất cả các giá trị thực của tham số m để hàm số
\(\: y = -x^3 + (m+3)x^2 - (m^2 + 2m)x - 2\) đạt cực đại tại \(x=2.\)
Lời giải:
Hàm số có tập xác định: \(D=\mathbb{R}\).
\(y' = -3x^2 + 2(m+3)x-(m^2 + 2m);\)
Để hàm số có cực trị tại \(x=2\) thì:
\(y'(2) = 0 \)
\(\Leftrightarrow - 12 + 4(m + 3) - {m^2} - 2m = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l} m = 0\\ m = 2 \end{array} \right.\)
Ta có: \(y'' = - 6x + 2(m + 3)\)
+ Với \(m=0\) thì \(y''(2)=-6<0.\)
+ Với \(m=2\) thì \(y''(2)=-2<0\).
Thứ lại với \(m=0\) và \(m=2\) hàm số đều đạt cực đại tại x = 2.