Ôn tập chương 4 Số phức
Video bài giảng
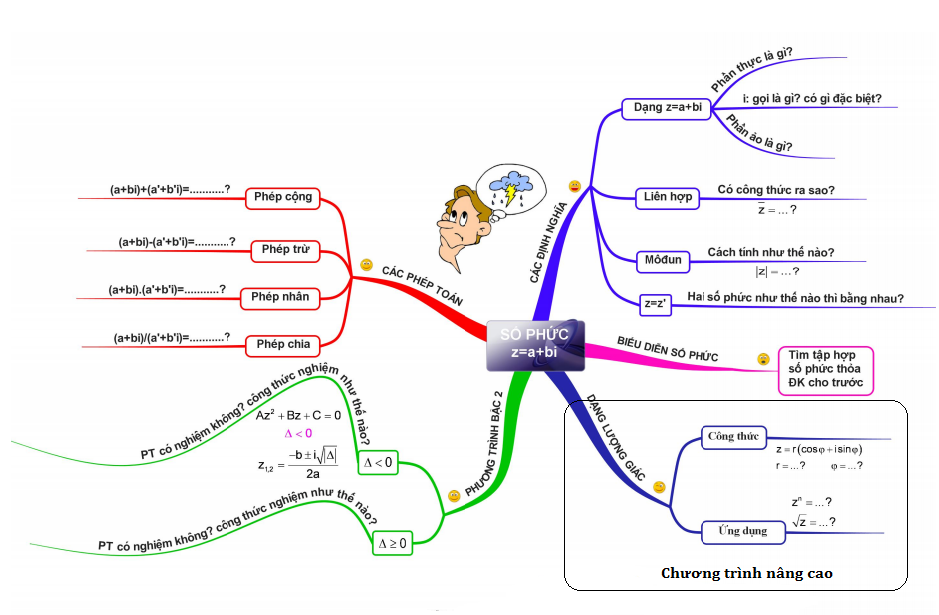
HỆ THỐNG HÓA KIẾN THỨC "SỐ PHỨC VÀ CÁC DẠNG TOÁN LIÊN QUAN"
Bài tập 1:
Tìm số phức z sao cho \((1 +2i)z\) là số thuần ảo và \(\left | 2.z-\bar{z} \right |=\sqrt{13}\).
Lời giải:
Giả sử \(z=a+bi \ (a,b\in R)\).
Khi đó \((1+2i)z=(1+2i)(a+bi)\)
\(=(a-2b)+(2a+b)i.\)
\((1 +2i)z\) là số thuần ảo khi và chỉ khi:
\(a-2b=0\Leftrightarrow a=2b\)
\(\left | 2.z-\bar{z} \right |=\left | a+3bi \right |=\left | 2b+3bi \right | \)
\(=\sqrt{13b^2}=\sqrt{13}\Leftrightarrow b=\pm 1.\)
Vậy có hai số phức thỏa mãn đề bài:
\(z=2+i;z=-2-i.\)
Bài tập 2:
Tìm phần thực và phần ảo của số phức z thoả mãn điều kiện \(z+(2+i)\bar{z}=3+5i.\)
Lời giải:
Giả sử \(z=a+bi(a,b\in R)\)
Ta có \(z+(1+i)\bar{z}=3+5i\)
\(\Leftrightarrow a+bi+(2+i)(a-bi)=3+5i\)
\(\Leftrightarrow 3a+b+(a-b)i=3+5i\)
\(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{3a + b = 3}\\
{a - b = 5}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{a = 2}\\
{b = - 3}
\end{array}} \right.\)
Vậy \(z=2-3i\).
Do đó phần thực của z là 2 và phần ảo của z là –3.
Bài tập 3:
Cho hai số phức \(z_1,z_2\) thỏa mãn
\(\left |z_1 \right |=\left |z_2 \right |=1,\left |z_1 +z_2 \right | =\sqrt{3}\).
Tính \(\left |z_1 -z_2 \right |.\)
Lời giải:
Đặt: \(z_1=a_1+b_1i;z_2=a_2+b_2i\)
\((a_1,a_2,b_1,b_2 \in R)\)
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{c}}
{\left| {{z_1}} \right| = \left| {{z_2}} \right| = 1}\\
{\left| {{z_1} + {z_2}} \right| = \sqrt 3 }
\end{array}} \right.\\
\Rightarrow \left\{ {\begin{array}{*{20}{c}}
{a_1^2 + b_1^2 = a_2^2 + b_2^2 = 1}\\
{{{({a_1} + {b_2})}^2} + {{({b_1} + {b_2})}^2} = 2}
\end{array}} \right.
\end{array}\)
\(\Leftrightarrow 2(a_1b_1+a_2b_2)=1\)
\(\Rightarrow (a_1-a_2)^2+(b_1-b_2)^2=1\)
Vậy \(\left | z_1-z_2 \right |=1.\)
Bài tập 4:
Cho số phức z thỏa mãn điều kiện
\((1+2i)z+(3+2i)\bar{z}=4+10i.\)
Tìm môđun của số phức \(w=z+2\bar{z}.\)
Lời giải:
Đặt \(z=a+bi(a,b\in R)\Rightarrow \bar{z}=a-bi\)
Ta có \((1+2i)z+(3+2i)\bar{z}=4+10i\)
\(\Leftrightarrow (1+2i)(a+bi)+\)
\((3+2i)(a-bi)(a-bi)=4+10i\)
\(\begin{array}{l}
\Leftrightarrow 4a + (4a - 2b)i = 4 + 10i\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{4a = 4}\\
{4a - 2b = 10}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{a = 1}\\
{b = - 3}
\end{array}} \right.
\end{array}\)
Do đó \(z= 1- 3i.\)
Ta có:
\(w=z+2\bar{z}=1-3i+2(1+3i)=3+3i.\)
Suy ra môđun của \(w\) là:
\(\left | w \right |=\sqrt{3^2+3^2}=3\sqrt{2}.\)
HỆ THỐNG HÓA KIẾN THỨC "SỐ PHỨC VÀ CÁC DẠNG TOÁN LIÊN QUAN"

Bài tập 1:
Tìm số phức z sao cho \((1 +2i)z\) là số thuần ảo và \(\left | 2.z-\bar{z} \right |=\sqrt{13}\).
Lời giải:
Giả sử \(z=a+bi \ (a,b\in R)\).
Khi đó \((1+2i)z=(1+2i)(a+bi)\)
\(=(a-2b)+(2a+b)i.\)
\((1 +2i)z\) là số thuần ảo khi và chỉ khi:
\(a-2b=0\Leftrightarrow a=2b\)
\(\left | 2.z-\bar{z} \right |=\left | a+3bi \right |=\left | 2b+3bi \right | \)
\(=\sqrt{13b^2}=\sqrt{13}\Leftrightarrow b=\pm 1.\)
Vậy có hai số phức thỏa mãn đề bài:
\(z=2+i;z=-2-i.\)
Bài tập 2:
Tìm phần thực và phần ảo của số phức z thoả mãn điều kiện \(z+(2+i)\bar{z}=3+5i.\)
Lời giải:
Giả sử \(z=a+bi(a,b\in R)\)
Ta có \(z+(1+i)\bar{z}=3+5i\)
\(\Leftrightarrow a+bi+(2+i)(a-bi)=3+5i\)
\(\Leftrightarrow 3a+b+(a-b)i=3+5i\)
\(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{3a + b = 3}\\
{a - b = 5}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{a = 2}\\
{b = - 3}
\end{array}} \right.\)
Vậy \(z=2-3i\).
Do đó phần thực của z là 2 và phần ảo của z là –3.
Bài tập 3:
Cho hai số phức \(z_1,z_2\) thỏa mãn
\(\left |z_1 \right |=\left |z_2 \right |=1,\left |z_1 +z_2 \right | =\sqrt{3}\).
Tính \(\left |z_1 -z_2 \right |.\)
Lời giải:
Đặt: \(z_1=a_1+b_1i;z_2=a_2+b_2i\)
\((a_1,a_2,b_1,b_2 \in R)\)
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{c}}
{\left| {{z_1}} \right| = \left| {{z_2}} \right| = 1}\\
{\left| {{z_1} + {z_2}} \right| = \sqrt 3 }
\end{array}} \right.\\
\Rightarrow \left\{ {\begin{array}{*{20}{c}}
{a_1^2 + b_1^2 = a_2^2 + b_2^2 = 1}\\
{{{({a_1} + {b_2})}^2} + {{({b_1} + {b_2})}^2} = 2}
\end{array}} \right.
\end{array}\)
\(\Leftrightarrow 2(a_1b_1+a_2b_2)=1\)
\(\Rightarrow (a_1-a_2)^2+(b_1-b_2)^2=1\)
Vậy \(\left | z_1-z_2 \right |=1.\)
Bài tập 4:
Cho số phức z thỏa mãn điều kiện
\((1+2i)z+(3+2i)\bar{z}=4+10i.\)
Tìm môđun của số phức \(w=z+2\bar{z}.\)
Lời giải:
Đặt \(z=a+bi(a,b\in R)\Rightarrow \bar{z}=a-bi\)
Ta có \((1+2i)z+(3+2i)\bar{z}=4+10i\)
\(\Leftrightarrow (1+2i)(a+bi)+\)
\((3+2i)(a-bi)(a-bi)=4+10i\)
\(\begin{array}{l}
\Leftrightarrow 4a + (4a - 2b)i = 4 + 10i\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{4a = 4}\\
{4a - 2b = 10}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{a = 1}\\
{b = - 3}
\end{array}} \right.
\end{array}\)
Do đó \(z= 1- 3i.\)
Ta có:
\(w=z+2\bar{z}=1-3i+2(1+3i)=3+3i.\)
Suy ra môđun của \(w\) là:
\(\left | w \right |=\sqrt{3^2+3^2}=3\sqrt{2}.\)