Bài 5: Khoảng cách
1. Khoảng cách từ một điểm tới một đường thẳng, đến một mặt phẳng
Khoảng cách từ điểm M đến đường thẳng a (hoặc đến mặt phẳng (P)) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên đường thẳng a (hoặc trên mp(P)).
\(d(O;a) = OH\)
.png)
\(d(O; (P))= OH\)
.png)
2. Khoảng cách giữa đường thẳng và mặt phẳng song song
Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm nào đó của a đến mặt phẳng (P).
\(d(a;(P)) = d(O,(P)) = OH\)
.png)
3. Khoảng cách giữa hai mặt phẳng song song
Cho (P) và (Q) là hai mặt phẳng song song. Khoảng cách giữa (P) và (Q) là khoảng cách từ một điểm bất kỳ trên mặt phẳng này đến mặt phẳng kia.
\(d((P);(Q)) = OH\)
.png)
4. Khoảng cách giữa hai đường thẳng chéo nhau
Cho a và b là hai đường thẳng chéo nhau. Khi đó khoảng cách giữa a và b là độ dài đoạn vuông góc chung của hai đường thẳng đó.
\(d(a;b) = AB\)
.png)
SƠ ĐỒ HỆ THỐNG HÓA KIẾN THỨC
"KHOẢNG CÁCH TRONG KHÔNG GIAN"
.png)
5. Bài tập minh họa
Ví dụ 1:
Cho mặt phẳng \(\left (\alpha \right )\), điểm A không thuộc mặt phẳng \(\left (\alpha \right )\), H là hình chiếu vuông góc của A lên mặt phẳng \(\left (\alpha \right )\), E là điểm thuộc AM sao cho: \(\frac{{ME}}{{MA}} = k.\)
a. Tính khoảng cách từ A đến mặt phẳng \(\left (\alpha \right )\).
b. Tính khoảng cách từ E đến mặt phẳng \(\left (\alpha \right )\), từ đó suy ra khoảng cách từ I – trung điểm của AM đến mặt phẳng \(\left (\alpha \right )\).
c. Gọi d là đường thẳng qua I song song với mặt phẳng \(\left (\alpha \right )\). Lấy J thuộc d, tính khoảng cách từ J đến mặt phẳng \(\left (\alpha \right )\).
d. Gọi C là chân đường vuông góc của J lên mặt phẳng \(\left (\alpha \right )\). D là trung điểm của JC. Tính khoảng cách từ D đến mặt phẳng \(\left (\alpha \right )\).
Hướng dẫn giải:
.png)
a) H là hình chiếu vuông góc của A lên mặt phẳng \(\left (\alpha \right )\) nên: \(d(A,\left (\alpha \right )) = AH = h\).
b) Gọi P là chân đường vuông góc của E lên mặt phẳng \(\left (\alpha \right )\).
Khi đó: \(d(E, \left (\alpha \right )) = EP\).
Ta có : EP // AH (đều vuông góc với mp \(\left (\alpha \right )\)) và M, P, H thẳng hàng.
Theo định lí Tallet ta có:
\(\frac{{EP}}{{AH}} = \frac{{ME}}{{MA}}=k\)
Khi đó: \(EP = k.AH\) hay \(d(E, (a)) = k.h\,(1)\).
Vì I là trung điểm của AM nên:
\(d(I,\left( \alpha \right)) = \frac{1}{2}.h\) (áp dụng kết quả (1) với \(k=\frac{1}{2}\)).
c) Ta có: IJCQ là hình chữ nhật nên \(IQ = JC\)
Do đó: \(d(J,\left( \alpha \right)) = d(I,\left( \alpha \right)) = \frac{1}{2}.h.\)
d) D là trung điểm của JC nên \(\frac{CD}{CJ}=\frac{1}{2}.\)
Suy ra:
\(d(Q,\left( \alpha \right)) = \frac{1}{2}d(J,\left( \alpha \right)) = \frac{1}{2}.\frac{1}{2}.h = \frac{1}{4}.h\).
Ví dụ 2:
Cho tứ diện SABC có tam giác ABC vuông cân đỉnh B, \(AB = a\), SA vuông góc với mặt phẳng (ABC) và \(SA = a\).
a. Chứng minh \((SAB)\bot (SBC)\).
b. Tính khoảng cách từ điểm A đến mp(SBC).
c. Gọi I là trung điểm của AB. Tính khoảng cách từ điểm I đến mp(SBC).
Hướng dẫn giải:
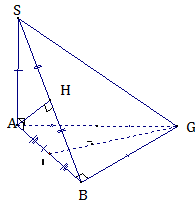
a) Theo giả thiết ta có: \(SA \bot (ABC)\).
Suy ra \(SA \bot BC\) (1).
Mà \(AB \bot BC\) (giả thiết) (2).
Từ (1) và (2) ta suy ra:
\(BC \bot (SAB)\Rightarrow (SBC) \bot (SAB).\)
b) Ta có: \((SAB)\cap (SBC)=SB\).
Kẻ \(AH \bot SB (H\in SB).\)
Do tam giác SAB vuông cân nên H là trung điểm của SB.
Khi đó:
\(AH \bot (SBC)\) nên \(d(A, (SBC))=AH\).
Xét tam giác SAB vuông cân tại A. Theo hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} \)
\(\Rightarrow AH = \frac{{a\sqrt 2 }}{2}.\)
c) Ta có:
\(AB\cap (SBC)=B\) và \(\frac{BI}{BA}=\frac{1}{2}\) (do I là trùng điểm của AB) nên:
\(d(I,(SBC)) = \frac{1}{2}d(A,(SBC)) \)
\(= \frac{1}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}.\)
Ví dụ 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\), \(SA = SB = SC = SD = a\sqrt2\). Tính khoảng cách giữa hai đường thẳng chéo nhau AD và SC.
Hướng dẫn giải:

Vì AD // BC
Nên \(d(AD, SC) = d(AD, (SBC)) \)
\(= d(A, (SBC))\).
Ta có \(AO\cap (SBC)=C\) và \(\frac{CO}{CA}=\frac{1}{2}\), do đó:
\(d(A,(SBC)) = 2.d(O,(SBC))\).
\(SO \bot (ABCD)\) nên \(SO \bot BC\)
Kẻ \(SI \bot BC\) thì I là trung điểm của BC.
Suy ra: \(BC \bot (SOI)\Rightarrow (SBC)\bot (SOI)\)
\((SBC)\cap (SOI)=SI\)
Kẻ \(OI \bot SI (H\in SI).\)
Khi đó \(d(O,(SBC)) = OH\)
Xét tam giác SOI vuông tại O, theo hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{J^2}}} + \frac{1}{{O{S^2}}}\) mà \(OJ = \frac{1}{2}.a;\)
\(SO = \sqrt {S{C^2} - C{O^2}} = \frac{{a\sqrt 6 }}{2}\)
Suy ra: \(OH = \frac{{\sqrt {42} }}{{14}}a.\)
Vậy: \(d(AD,SC) = 2.\frac{{\sqrt {42} }}{{14}}a = \frac{{\sqrt {42} }}{7}.a.\)
1. Khoảng cách từ một điểm tới một đường thẳng, đến một mặt phẳng
Khoảng cách từ điểm M đến đường thẳng a (hoặc đến mặt phẳng (P)) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên đường thẳng a (hoặc trên mp(P)).
\(d(O;a) = OH\)
.png)
\(d(O; (P))= OH\)
.png)
2. Khoảng cách giữa đường thẳng và mặt phẳng song song
Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm nào đó của a đến mặt phẳng (P).
\(d(a;(P)) = d(O,(P)) = OH\)
.png)
3. Khoảng cách giữa hai mặt phẳng song song
Cho (P) và (Q) là hai mặt phẳng song song. Khoảng cách giữa (P) và (Q) là khoảng cách từ một điểm bất kỳ trên mặt phẳng này đến mặt phẳng kia.
\(d((P);(Q)) = OH\)
.png)
4. Khoảng cách giữa hai đường thẳng chéo nhau
Cho a và b là hai đường thẳng chéo nhau. Khi đó khoảng cách giữa a và b là độ dài đoạn vuông góc chung của hai đường thẳng đó.
\(d(a;b) = AB\)
.png)
SƠ ĐỒ HỆ THỐNG HÓA KIẾN THỨC
"KHOẢNG CÁCH TRONG KHÔNG GIAN"
.png)
5. Bài tập minh họa
Ví dụ 1:
Cho mặt phẳng \(\left (\alpha \right )\), điểm A không thuộc mặt phẳng \(\left (\alpha \right )\), H là hình chiếu vuông góc của A lên mặt phẳng \(\left (\alpha \right )\), E là điểm thuộc AM sao cho: \(\frac{{ME}}{{MA}} = k.\)
a. Tính khoảng cách từ A đến mặt phẳng \(\left (\alpha \right )\).
b. Tính khoảng cách từ E đến mặt phẳng \(\left (\alpha \right )\), từ đó suy ra khoảng cách từ I – trung điểm của AM đến mặt phẳng \(\left (\alpha \right )\).
c. Gọi d là đường thẳng qua I song song với mặt phẳng \(\left (\alpha \right )\). Lấy J thuộc d, tính khoảng cách từ J đến mặt phẳng \(\left (\alpha \right )\).
d. Gọi C là chân đường vuông góc của J lên mặt phẳng \(\left (\alpha \right )\). D là trung điểm của JC. Tính khoảng cách từ D đến mặt phẳng \(\left (\alpha \right )\).
Hướng dẫn giải:
.png)
a) H là hình chiếu vuông góc của A lên mặt phẳng \(\left (\alpha \right )\) nên: \(d(A,\left (\alpha \right )) = AH = h\).
b) Gọi P là chân đường vuông góc của E lên mặt phẳng \(\left (\alpha \right )\).
Khi đó: \(d(E, \left (\alpha \right )) = EP\).
Ta có : EP // AH (đều vuông góc với mp \(\left (\alpha \right )\)) và M, P, H thẳng hàng.
Theo định lí Tallet ta có:
\(\frac{{EP}}{{AH}} = \frac{{ME}}{{MA}}=k\)
Khi đó: \(EP = k.AH\) hay \(d(E, (a)) = k.h\,(1)\).
Vì I là trung điểm của AM nên:
\(d(I,\left( \alpha \right)) = \frac{1}{2}.h\) (áp dụng kết quả (1) với \(k=\frac{1}{2}\)).
c) Ta có: IJCQ là hình chữ nhật nên \(IQ = JC\)
Do đó: \(d(J,\left( \alpha \right)) = d(I,\left( \alpha \right)) = \frac{1}{2}.h.\)
d) D là trung điểm của JC nên \(\frac{CD}{CJ}=\frac{1}{2}.\)
Suy ra:
\(d(Q,\left( \alpha \right)) = \frac{1}{2}d(J,\left( \alpha \right)) = \frac{1}{2}.\frac{1}{2}.h = \frac{1}{4}.h\).
Ví dụ 2:
Cho tứ diện SABC có tam giác ABC vuông cân đỉnh B, \(AB = a\), SA vuông góc với mặt phẳng (ABC) và \(SA = a\).
a. Chứng minh \((SAB)\bot (SBC)\).
b. Tính khoảng cách từ điểm A đến mp(SBC).
c. Gọi I là trung điểm của AB. Tính khoảng cách từ điểm I đến mp(SBC).
Hướng dẫn giải:

a) Theo giả thiết ta có: \(SA \bot (ABC)\).
Suy ra \(SA \bot BC\) (1).
Mà \(AB \bot BC\) (giả thiết) (2).
Từ (1) và (2) ta suy ra:
\(BC \bot (SAB)\Rightarrow (SBC) \bot (SAB).\)
b) Ta có: \((SAB)\cap (SBC)=SB\).
Kẻ \(AH \bot SB (H\in SB).\)
Do tam giác SAB vuông cân nên H là trung điểm của SB.
Khi đó:
\(AH \bot (SBC)\) nên \(d(A, (SBC))=AH\).
Xét tam giác SAB vuông cân tại A. Theo hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} \)
\(\Rightarrow AH = \frac{{a\sqrt 2 }}{2}.\)
c) Ta có:
\(AB\cap (SBC)=B\) và \(\frac{BI}{BA}=\frac{1}{2}\) (do I là trùng điểm của AB) nên:
\(d(I,(SBC)) = \frac{1}{2}d(A,(SBC)) \)
\(= \frac{1}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}.\)
Ví dụ 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\), \(SA = SB = SC = SD = a\sqrt2\). Tính khoảng cách giữa hai đường thẳng chéo nhau AD và SC.
Hướng dẫn giải:

Vì AD // BC
Nên \(d(AD, SC) = d(AD, (SBC)) \)
\(= d(A, (SBC))\).
Ta có \(AO\cap (SBC)=C\) và \(\frac{CO}{CA}=\frac{1}{2}\), do đó:
\(d(A,(SBC)) = 2.d(O,(SBC))\).
\(SO \bot (ABCD)\) nên \(SO \bot BC\)
Kẻ \(SI \bot BC\) thì I là trung điểm của BC.
Suy ra: \(BC \bot (SOI)\Rightarrow (SBC)\bot (SOI)\)
\((SBC)\cap (SOI)=SI\)
Kẻ \(OI \bot SI (H\in SI).\)
Khi đó \(d(O,(SBC)) = OH\)
Xét tam giác SOI vuông tại O, theo hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{J^2}}} + \frac{1}{{O{S^2}}}\) mà \(OJ = \frac{1}{2}.a;\)
\(SO = \sqrt {S{C^2} - C{O^2}} = \frac{{a\sqrt 6 }}{2}\)
Suy ra: \(OH = \frac{{\sqrt {42} }}{{14}}a.\)
Vậy: \(d(AD,SC) = 2.\frac{{\sqrt {42} }}{{14}}a = \frac{{\sqrt {42} }}{7}.a.\)