Bài 1: Vectơ trong không gian
1. Các phép tính vectơ
a) Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì:
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD}.\)
b) Quy tắc ba điểm đối với phép cộng vectơ
Cho ba điểm A, B, C bất kì thì
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC}\).
(1).png)
Quy tắc ba điểm với phép trừ vectơ:
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA}\)
c) Quy tắc hình hộp
Cho hình hộp ABCD. A’B’C’D’ thì
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {{\rm{AA'}}}\).
d. Quy tắc nhận vectơ với một số:
Cho vectơ \(\vec a\) và một số thực \(k \ne 0\) ta được vectơ \(k \vec a\) có các tính chất sau:
- \(\left| {k.\overrightarrow a } \right| = \left| k \right|.\left| {\overrightarrow a } \right|{\rm{ }}\).
- Nếu \(k > 0\) thì \(\vec a\) cùng hướng với \(k \vec a\).
- Nếu \(k < 0\) thì \(k \vec a\) ngược hướng với \(k \vec a\).
2. Điều kiện đồng phẳng của ba vectơ
a) Vectơ cùng phương
Điều kiện cần và đủ để hai vectơ \(\vec a, \vec b\) cùng phương là có một số thực k để \(\overrightarrow a = k.\overrightarrow b\).
b) Vectơ đồng phẳng
- Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
- Điều kiện để ba vectơ đồng phẳng: Cho \(\vec a, \vec b\) là hai vectơ không cùng phương và vectơ \(\vec c\). Ba vectơ \(\vec a, \vec b\) và \(\vec c\) đồng phẳng khi và chỉ khi có hai số thực k, l sao cho: \(\overrightarrow c = k.\overrightarrow a + l.\overrightarrow b .\)
3. Bài tập minh họa
Ví dụ 1:
Cho hình lăng trụ ABC.A’B’C’. Hãy nêu tên các vecto bằng nhau có điểm đầu và điểm cuối là các đỉnh của hình lăng trụ.
Hướng dẫn giải:
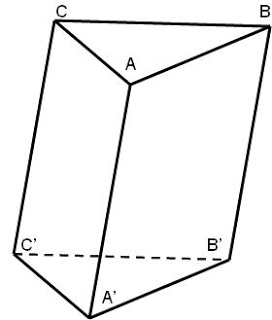
Theo tính chất hình lăng trụ ta có:
\(\begin{array}{*{20}{l}}
{\overrightarrow {AB} = \overrightarrow {A'B'} ;\overrightarrow {BC} = \overrightarrow {B'C'} ;\overrightarrow {CA} = \overrightarrow {C'A'} }\\
{\overrightarrow {AB} = - \overrightarrow {BA} ;\overrightarrow {BC} = - \overrightarrow {CB} ;\overrightarrow {CA} = - \overrightarrow {AC} }\\
\begin{array}{l}
\overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = - \overrightarrow {A'A} = - \overrightarrow {B'B} \\
\,\,\,\,\,\,\,\,\,\, = - \overrightarrow {C'C} .
\end{array}
\end{array}\)
Ví dụ 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\).
Hướng dẫn giải:
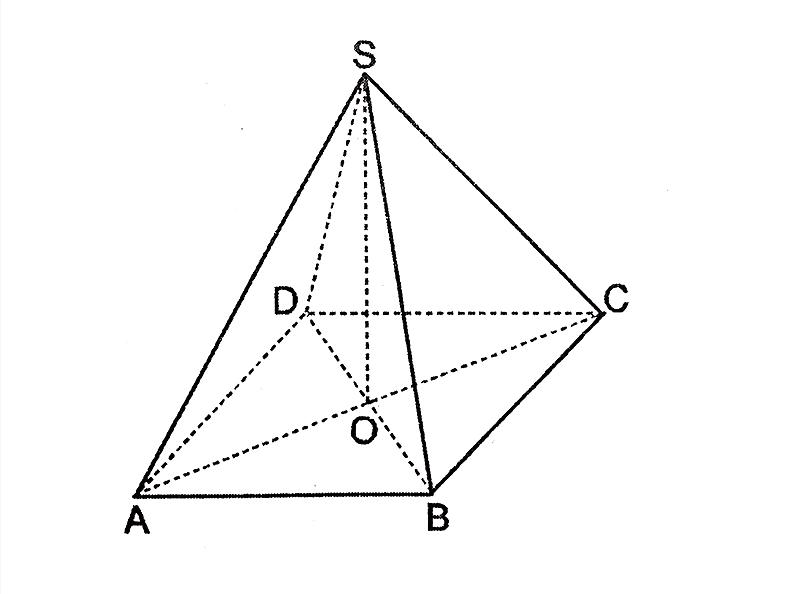
Gọi O là tâm của hình bình hành ABCD. Ta có:
\(\begin{array}{l} \overrightarrow {SA} + \overrightarrow {AO} = \overrightarrow {SO} \\ \overrightarrow {SC} + \overrightarrow {CO} = \overrightarrow {SO} \\ \Rightarrow \overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} (1) \end{array}\)
Theo quy tắc hình bình hành:
\(\overrightarrow {{\rm{SB}}} + \overrightarrow {SD} = 2\overrightarrow {SO} (2)\)
Từ (1) và (2) ta có:
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\).
Ví dụ 3:
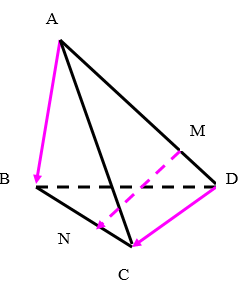
Cho tứ diện ABCD. Trên cạnh AD lấy điểm M sao cho \(\overrightarrow {AM} = 3\overrightarrow {MD}\) và trên cạnh BC lấy điểm N sao cho \(\overrightarrow {NB} = - 3\overrightarrow {NC}\). Chứng tỏ rằng \(\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {MN}\) đồng phẳng.
Hướng dẫn giải:
Theo giả thiết ta có:
\(\overrightarrow {AM} = 3\overrightarrow {MD} \Rightarrow \overrightarrow {MA} = - \overrightarrow {MD}\)
và \(\overrightarrow {{\rm{NB}}} = - 3\overrightarrow {NC}\)
Mà: \(\overrightarrow {{\rm{MN}}} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN}\)
và \(\overrightarrow {{\rm{MN}}} = \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} (1)\)
\(\Rightarrow 3\overrightarrow {MN} = 3\overrightarrow {MD} + 3\overrightarrow {DC} + 3\overrightarrow {CN} (2)\)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
(1) + (2) \Rightarrow 4\overrightarrow {MN} = \overrightarrow {MA} + 3\overrightarrow {MD} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \overrightarrow {AB} + 3\overrightarrow {DC} + \overrightarrow {BN} + 3\overrightarrow {CN}
\end{array}\\
\begin{array}{l}
\Leftrightarrow 4\overrightarrow {MN} = \overrightarrow {MA} + 3\overrightarrow {MD} \\
\Leftrightarrow \overrightarrow {MN} = \frac{1}{4}\overrightarrow {MA} + \frac{3}{4}\overrightarrow {MD}
\end{array}
\end{array}\)
Hệ thức trên chứng tỏ:
\(\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {MN}\) đồng phẳng.
1. Các phép tính vectơ
a) Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì:
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD}.\)
b) Quy tắc ba điểm đối với phép cộng vectơ
Cho ba điểm A, B, C bất kì thì
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC}\).
(1).png)
Quy tắc ba điểm với phép trừ vectơ:
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA}\)
c) Quy tắc hình hộp
Cho hình hộp ABCD. A’B’C’D’ thì
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {{\rm{AA'}}}\).
d. Quy tắc nhận vectơ với một số:
Cho vectơ \(\vec a\) và một số thực \(k \ne 0\) ta được vectơ \(k \vec a\) có các tính chất sau:
- \(\left| {k.\overrightarrow a } \right| = \left| k \right|.\left| {\overrightarrow a } \right|{\rm{ }}\).
- Nếu \(k > 0\) thì \(\vec a\) cùng hướng với \(k \vec a\).
- Nếu \(k < 0\) thì \(k \vec a\) ngược hướng với \(k \vec a\).
2. Điều kiện đồng phẳng của ba vectơ
a) Vectơ cùng phương
Điều kiện cần và đủ để hai vectơ \(\vec a, \vec b\) cùng phương là có một số thực k để \(\overrightarrow a = k.\overrightarrow b\).
b) Vectơ đồng phẳng
- Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
- Điều kiện để ba vectơ đồng phẳng: Cho \(\vec a, \vec b\) là hai vectơ không cùng phương và vectơ \(\vec c\). Ba vectơ \(\vec a, \vec b\) và \(\vec c\) đồng phẳng khi và chỉ khi có hai số thực k, l sao cho: \(\overrightarrow c = k.\overrightarrow a + l.\overrightarrow b .\)
3. Bài tập minh họa
Ví dụ 1:
Cho hình lăng trụ ABC.A’B’C’. Hãy nêu tên các vecto bằng nhau có điểm đầu và điểm cuối là các đỉnh của hình lăng trụ.
Hướng dẫn giải:

Theo tính chất hình lăng trụ ta có:
\(\begin{array}{*{20}{l}}
{\overrightarrow {AB} = \overrightarrow {A'B'} ;\overrightarrow {BC} = \overrightarrow {B'C'} ;\overrightarrow {CA} = \overrightarrow {C'A'} }\\
{\overrightarrow {AB} = - \overrightarrow {BA} ;\overrightarrow {BC} = - \overrightarrow {CB} ;\overrightarrow {CA} = - \overrightarrow {AC} }\\
\begin{array}{l}
\overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = - \overrightarrow {A'A} = - \overrightarrow {B'B} \\
\,\,\,\,\,\,\,\,\,\, = - \overrightarrow {C'C} .
\end{array}
\end{array}\)
Ví dụ 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\).
Hướng dẫn giải:

Gọi O là tâm của hình bình hành ABCD. Ta có:
\(\begin{array}{l} \overrightarrow {SA} + \overrightarrow {AO} = \overrightarrow {SO} \\ \overrightarrow {SC} + \overrightarrow {CO} = \overrightarrow {SO} \\ \Rightarrow \overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} (1) \end{array}\)
Theo quy tắc hình bình hành:
\(\overrightarrow {{\rm{SB}}} + \overrightarrow {SD} = 2\overrightarrow {SO} (2)\)
Từ (1) và (2) ta có:
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\).
Ví dụ 3:
Cho tứ diện ABCD. Trên cạnh AD lấy điểm M sao cho \(\overrightarrow {AM} = 3\overrightarrow {MD}\) và trên cạnh BC lấy điểm N sao cho \(\overrightarrow {NB} = - 3\overrightarrow {NC}\). Chứng tỏ rằng \(\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {MN}\) đồng phẳng.
Hướng dẫn giải:
Theo giả thiết ta có:
\(\overrightarrow {AM} = 3\overrightarrow {MD} \Rightarrow \overrightarrow {MA} = - \overrightarrow {MD}\)
và \(\overrightarrow {{\rm{NB}}} = - 3\overrightarrow {NC}\)
Mà: \(\overrightarrow {{\rm{MN}}} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN}\)
và \(\overrightarrow {{\rm{MN}}} = \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} (1)\)
\(\Rightarrow 3\overrightarrow {MN} = 3\overrightarrow {MD} + 3\overrightarrow {DC} + 3\overrightarrow {CN} (2)\)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
(1) + (2) \Rightarrow 4\overrightarrow {MN} = \overrightarrow {MA} + 3\overrightarrow {MD} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \overrightarrow {AB} + 3\overrightarrow {DC} + \overrightarrow {BN} + 3\overrightarrow {CN}
\end{array}\\
\begin{array}{l}
\Leftrightarrow 4\overrightarrow {MN} = \overrightarrow {MA} + 3\overrightarrow {MD} \\
\Leftrightarrow \overrightarrow {MN} = \frac{1}{4}\overrightarrow {MA} + \frac{3}{4}\overrightarrow {MD}
\end{array}
\end{array}\)
Hệ thức trên chứng tỏ:
\(\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {MN}\) đồng phẳng.
.PNG)
.PNG)
.PNG)