Bài 2: Hai đường thẳng vuông góc
1. Góc giữa hai vectơ
Cho \(\vec u\) và \(\vec v\) là hai vectơ trong không gian. Từ một điểm A bất kì vẽ \(\overrightarrow {AB} = \overrightarrow u ,\overrightarrow {AC} = \overrightarrow v\). Khi đó ta gọi góc \(\widehat {BAC}(0 \le \widehat {BAC} \le {180^0})\) là góc giữa hai vecto vectơ \(\vec u\) và \(\vec v\), kí hiệu là \(\left ( \vec u ;\vec v \right )\). Ta có: \(\left ( \vec u ;\vec v \right )=\widehat {BAC}\).
2. Tích vô hướng của hai vectơ
a) Định nghĩa tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ \(\vec u\) và \(\vec v\) đều khác vectơ-không là một số được kí hiệu là \(\vec u .\vec v\) xác dịnh bởi:
\(\vec u.\vec v = \left| {\vec u} \right|.\left| {\vec v} \right|.\cos (\overrightarrow u .\vec v)\)
Nếu \(\vec u= \vec0\) hoặc \(\vec v= \vec0\) thì ta quy ước
\(\vec u.\vec v=0.\)
b) Tính chất tích vô hướng của hai vectơ
Với ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\) trong không gian và với mọi số k ta có:
- \(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a\) (tính chất giao hoán).
- \(\overrightarrow a (\overrightarrow b + \overrightarrow c ) = \overrightarrow a .\overrightarrow b + \overrightarrow a .\overrightarrow c\) (tính chất phân phối).
- \((k.\overrightarrow a ).\overrightarrow b = k.(\overrightarrow a .\overrightarrow b ) = \overrightarrow a .k\overrightarrow b .\)
- \({\overrightarrow a ^2} \ge 0,{\overrightarrow a ^2} = 0 \Leftrightarrow \overrightarrow a = \overrightarrow 0.\)
c) Ứng dụng của tích vô hướng
Xác định góc giữa hai vectơ \(\vec u\) và \(\vec v\) bằng \(\cos (\overrightarrow u .\vec v)\) theo công thức:
\(\cos (\overrightarrow u .\vec v) = \frac{{\vec u.\vec v}}{{\left| {\vec u} \right|\left| {\vec v} \right|}}\)
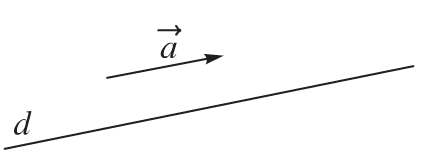
3. Vectơ chỉ phương của đường thẳng
Vectơ \(\overrightarrow a \ne \overrightarrow 0\) được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ \(\overrightarrow a\) song song hoặc trùng với đường thẳng d.
Nếu \(\overrightarrow a\) là vectơ chỉ phương của đường thẳng d thì vectơ \(k\overrightarrow a\) với \(k \ne 0\) cũng là một vectơ chỉ phương của d.
Một đường thẳng d trong không gian hoàn toàn xác định được nếu biết một điểm A thuộc d và một vectơ chỉ phương \(\overrightarrow a\) của d.
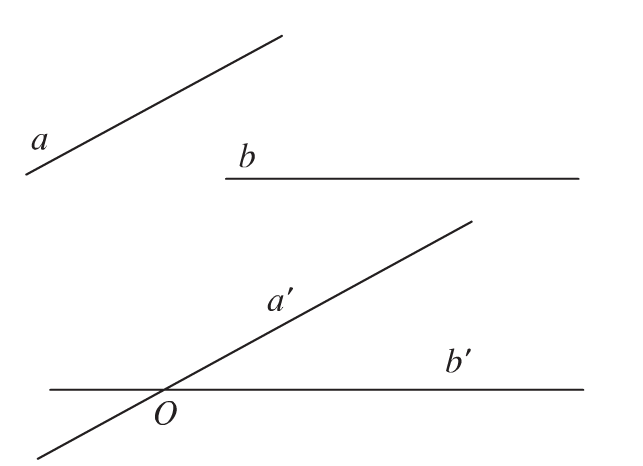
4. Góc giữa hai đường thẳng
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm bất kì lần lượt song song với a và b.
5. Hai đường thẳng vuông góc
a) Định nghĩa
Hai đường thẳng a và b gọi là vuông góc với nhau nếu góc giữa chúng bằng 900.
Ta kí hiệu là: \(b \bot a\) hoặc \(a \bot b.\)
b) Tính chất
- Nếu \(\vec u\) và \(\vec v\) lần lượt là các vectơ chỉ phương của hai đường thẳng a và b thì: \(a \bot b \Leftrightarrow \overrightarrow u .\overrightarrow v = 0.\)
- Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
- Hai đường thẳng vuông góc nhau thì có thể cắt nhau hoặc chéo nhau.
6. Bài tập minh họa
Ví dụ 1:
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:
a) \(\overrightarrow {AB} ,\overrightarrow {EG} .\)
c) \(\overrightarrow {AB} ,\overrightarrow {DH}\).
Hướng dẫn giải:
.png)
a) Vì EG // AC nên góc giữa
\(\overrightarrow {AB} ,\overrightarrow {EG}\) cũng bằng góc giữa
\(\overrightarrow {AB}\) và \(\overrightarrow {AC}\)
Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = {45^0}.\)
b) Vì AB // DG nên góc giữa \(\overrightarrow {AB} ,\overrightarrow {DH}\) cũng bằng góc giữa \(\overrightarrow {DC}\) và \(\overrightarrow {DH}\)
Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = {45^0}.\)
Ví dụ 2:
Cho hình chóp tam giác S.ABC có SA = SB = SC và có \(\widehat {{\rm{ASB}}} = \widehat {BSC} = \widehat {CSA}.\)
Chứng minh rằng: \(SA \bot BC, SB\bot AC, SC \bot AB.\)
Hướng dẫn giải:
Xét các tích vô hướng:
\(\overrightarrow {SA} .\overrightarrow {BC} ,\overrightarrow {SB} .\overrightarrow {AC} ,\overrightarrow {SC} .\overrightarrow {AB} .\)
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .(\overrightarrow {SC} - \overrightarrow {SB} )\\
= \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB}
\end{array}\\
\begin{array}{l}
= \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.\cos \widehat {CSA}\\
\,\,\,\,\,\,\,\,\, - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|\cos \widehat {ASB}
\end{array}
\end{array}\)
Theo giá thuyết: \(\left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right|\)
Và: \(\cos \widehat {CSA} = \cos \widehat {ASB} \Rightarrow \overrightarrow {SA} .\overrightarrow {BC} = 0\)
Vậy: \(SA \bot BC.\)
Chứng minh tương tự ta có:
\(SB\bot AC, SC \bot AB.\)
Ví dụ 3:
Cho tứ diện ABCD có AB ⊥ AC và AB ⊥ BD. Gọi P và Q lần lượt là trung điểm của AB và CD. Chứng minh rằng AB và PQ là hai đường thẳng vuông góc với nhau.
Hướng dẫn giải:
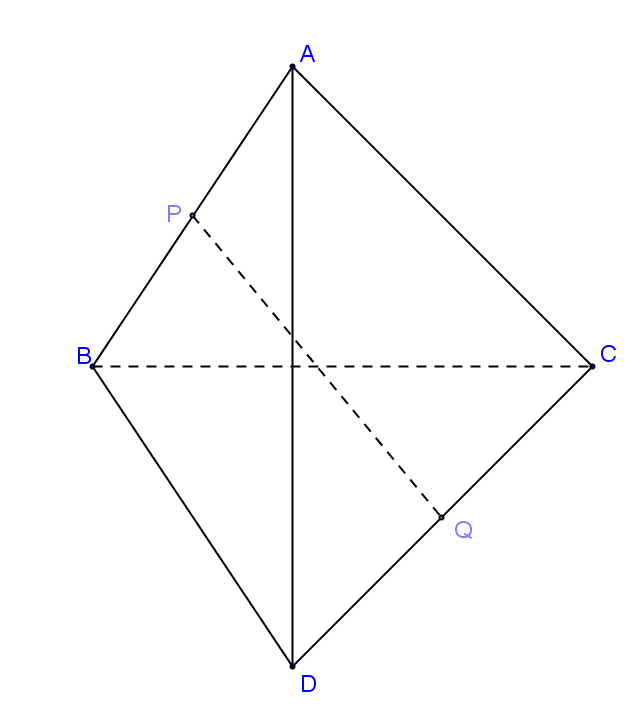
Ta có: \(\overrightarrow {PQ} = \overrightarrow {PA} + \overrightarrow {AC} + \overrightarrow {CQ}\)
Và: \(\overrightarrow {PQ} = \overrightarrow {PB} + \overrightarrow {BD} + \overrightarrow {DQ}\)
Do đó: \(2\overrightarrow {PQ} = \overrightarrow {AC} + \overrightarrow {BD}\)
Vậy: \(2.\overrightarrow {PQ} .\overrightarrow {AB} = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right).\overrightarrow {AB}\)
\(= \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {BD} .\overrightarrow {AB} = 0\)
Hay \(\overrightarrow {PQ} .\overrightarrow {AB} = 0\) Tức là: \(PQ \bot AB.\)
Ví dụ 4:
Cho tứ diện ABCD có AB=AC=AD=a, \(\widehat {BAC} = \widehat {BAD} = {60^0}.\).
a) Chứng minh rằng AB vuông góc CD.
b) Nếu I, J lần lượt là trung điểm của AB và CD thì \(AB \bot IJ.\)
Hướng dẫn giải:
.png)
a) Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)\\
= \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC}
\end{array}\\
\begin{array}{l}
= \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD\\
\,\,\,\, - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC
\end{array}
\end{array}\)
Mặt khác ta có:
\(AB = AC = AD,\widehat {BAC} = \widehat {BAD}\)
Do đó:
\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC = 0
\end{array}\)
Vậy AB vuông góc với CD.
b) Do I, J là trung điểm của AB và CD nên ta có: \(\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\)
Do đó:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} \overrightarrow {BC} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} \overrightarrow {BA} + \overrightarrow {AB} .\overrightarrow {AC} } \right)
\end{array}\\
\begin{array}{l}
= \frac{1}{2}(\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|\cos {60^0} - {\overrightarrow {AB} ^2}\\
\,\,\,\,\,\,\,\,\,\,\,\, + \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|\cos {60^0})
\end{array}\\
{ = \frac{1}{2}\left( {\frac{1}{2}{a^2} - {a^2} + \frac{1}{2}{a^2}} \right) = 0}
\end{array}\)
Vậy AB và IJ vuông góc nhau.
1. Góc giữa hai vectơ
Cho \(\vec u\) và \(\vec v\) là hai vectơ trong không gian. Từ một điểm A bất kì vẽ \(\overrightarrow {AB} = \overrightarrow u ,\overrightarrow {AC} = \overrightarrow v\). Khi đó ta gọi góc \(\widehat {BAC}(0 \le \widehat {BAC} \le {180^0})\) là góc giữa hai vecto vectơ \(\vec u\) và \(\vec v\), kí hiệu là \(\left ( \vec u ;\vec v \right )\). Ta có: \(\left ( \vec u ;\vec v \right )=\widehat {BAC}\).
2. Tích vô hướng của hai vectơ
a) Định nghĩa tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ \(\vec u\) và \(\vec v\) đều khác vectơ-không là một số được kí hiệu là \(\vec u .\vec v\) xác dịnh bởi:
\(\vec u.\vec v = \left| {\vec u} \right|.\left| {\vec v} \right|.\cos (\overrightarrow u .\vec v)\)
Nếu \(\vec u= \vec0\) hoặc \(\vec v= \vec0\) thì ta quy ước
\(\vec u.\vec v=0.\)
b) Tính chất tích vô hướng của hai vectơ
Với ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\) trong không gian và với mọi số k ta có:
- \(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a\) (tính chất giao hoán).
- \(\overrightarrow a (\overrightarrow b + \overrightarrow c ) = \overrightarrow a .\overrightarrow b + \overrightarrow a .\overrightarrow c\) (tính chất phân phối).
- \((k.\overrightarrow a ).\overrightarrow b = k.(\overrightarrow a .\overrightarrow b ) = \overrightarrow a .k\overrightarrow b .\)
- \({\overrightarrow a ^2} \ge 0,{\overrightarrow a ^2} = 0 \Leftrightarrow \overrightarrow a = \overrightarrow 0.\)
c) Ứng dụng của tích vô hướng
Xác định góc giữa hai vectơ \(\vec u\) và \(\vec v\) bằng \(\cos (\overrightarrow u .\vec v)\) theo công thức:
\(\cos (\overrightarrow u .\vec v) = \frac{{\vec u.\vec v}}{{\left| {\vec u} \right|\left| {\vec v} \right|}}\)
3. Vectơ chỉ phương của đường thẳng
Vectơ \(\overrightarrow a \ne \overrightarrow 0\) được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ \(\overrightarrow a\) song song hoặc trùng với đường thẳng d.
Nếu \(\overrightarrow a\) là vectơ chỉ phương của đường thẳng d thì vectơ \(k\overrightarrow a\) với \(k \ne 0\) cũng là một vectơ chỉ phương của d.
Một đường thẳng d trong không gian hoàn toàn xác định được nếu biết một điểm A thuộc d và một vectơ chỉ phương \(\overrightarrow a\) của d.
4. Góc giữa hai đường thẳng
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm bất kì lần lượt song song với a và b.
5. Hai đường thẳng vuông góc
a) Định nghĩa
Hai đường thẳng a và b gọi là vuông góc với nhau nếu góc giữa chúng bằng 900.
Ta kí hiệu là: \(b \bot a\) hoặc \(a \bot b.\)
b) Tính chất
- Nếu \(\vec u\) và \(\vec v\) lần lượt là các vectơ chỉ phương của hai đường thẳng a và b thì: \(a \bot b \Leftrightarrow \overrightarrow u .\overrightarrow v = 0.\)
- Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
- Hai đường thẳng vuông góc nhau thì có thể cắt nhau hoặc chéo nhau.
6. Bài tập minh họa
Ví dụ 1:
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:
a) \(\overrightarrow {AB} ,\overrightarrow {EG} .\)
c) \(\overrightarrow {AB} ,\overrightarrow {DH}\).
Hướng dẫn giải:
.png)
a) Vì EG // AC nên góc giữa
\(\overrightarrow {AB} ,\overrightarrow {EG}\) cũng bằng góc giữa
\(\overrightarrow {AB}\) và \(\overrightarrow {AC}\)
Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = {45^0}.\)
b) Vì AB // DG nên góc giữa \(\overrightarrow {AB} ,\overrightarrow {DH}\) cũng bằng góc giữa \(\overrightarrow {DC}\) và \(\overrightarrow {DH}\)
Vậy \(\left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {DH} } \right) = {45^0}.\)
Ví dụ 2:
Cho hình chóp tam giác S.ABC có SA = SB = SC và có \(\widehat {{\rm{ASB}}} = \widehat {BSC} = \widehat {CSA}.\)
Chứng minh rằng: \(SA \bot BC, SB\bot AC, SC \bot AB.\)
Hướng dẫn giải:
Xét các tích vô hướng:
\(\overrightarrow {SA} .\overrightarrow {BC} ,\overrightarrow {SB} .\overrightarrow {AC} ,\overrightarrow {SC} .\overrightarrow {AB} .\)
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .(\overrightarrow {SC} - \overrightarrow {SB} )\\
= \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB}
\end{array}\\
\begin{array}{l}
= \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.\cos \widehat {CSA}\\
\,\,\,\,\,\,\,\,\, - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|\cos \widehat {ASB}
\end{array}
\end{array}\)
Theo giá thuyết: \(\left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right|\)
Và: \(\cos \widehat {CSA} = \cos \widehat {ASB} \Rightarrow \overrightarrow {SA} .\overrightarrow {BC} = 0\)
Vậy: \(SA \bot BC.\)
Chứng minh tương tự ta có:
\(SB\bot AC, SC \bot AB.\)
Ví dụ 3:
Cho tứ diện ABCD có AB ⊥ AC và AB ⊥ BD. Gọi P và Q lần lượt là trung điểm của AB và CD. Chứng minh rằng AB và PQ là hai đường thẳng vuông góc với nhau.
Hướng dẫn giải:

Ta có: \(\overrightarrow {PQ} = \overrightarrow {PA} + \overrightarrow {AC} + \overrightarrow {CQ}\)
Và: \(\overrightarrow {PQ} = \overrightarrow {PB} + \overrightarrow {BD} + \overrightarrow {DQ}\)
Do đó: \(2\overrightarrow {PQ} = \overrightarrow {AC} + \overrightarrow {BD}\)
Vậy: \(2.\overrightarrow {PQ} .\overrightarrow {AB} = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right).\overrightarrow {AB}\)
\(= \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {BD} .\overrightarrow {AB} = 0\)
Hay \(\overrightarrow {PQ} .\overrightarrow {AB} = 0\) Tức là: \(PQ \bot AB.\)
Ví dụ 4:
Cho tứ diện ABCD có AB=AC=AD=a, \(\widehat {BAC} = \widehat {BAD} = {60^0}.\).
a) Chứng minh rằng AB vuông góc CD.
b) Nếu I, J lần lượt là trung điểm của AB và CD thì \(AB \bot IJ.\)
Hướng dẫn giải:
.png)
a) Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)\\
= \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC}
\end{array}\\
\begin{array}{l}
= \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD\\
\,\,\,\, - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC
\end{array}
\end{array}\)
Mặt khác ta có:
\(AB = AC = AD,\widehat {BAC} = \widehat {BAD}\)
Do đó:
\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos BAD\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos BAC = 0
\end{array}\)
Vậy AB vuông góc với CD.
b) Do I, J là trung điểm của AB và CD nên ta có: \(\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\)
Do đó:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} \overrightarrow {BC} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} \overrightarrow {BA} + \overrightarrow {AB} .\overrightarrow {AC} } \right)
\end{array}\\
\begin{array}{l}
= \frac{1}{2}(\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|\cos {60^0} - {\overrightarrow {AB} ^2}\\
\,\,\,\,\,\,\,\,\,\,\,\, + \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|\cos {60^0})
\end{array}\\
{ = \frac{1}{2}\left( {\frac{1}{2}{a^2} - {a^2} + \frac{1}{2}{a^2}} \right) = 0}
\end{array}\)
Vậy AB và IJ vuông góc nhau.
.PNG)