Ôn tập chương 5 Đạo hàm
1. Hệ thống kiến thức chương V Đại số và Giải tích 11
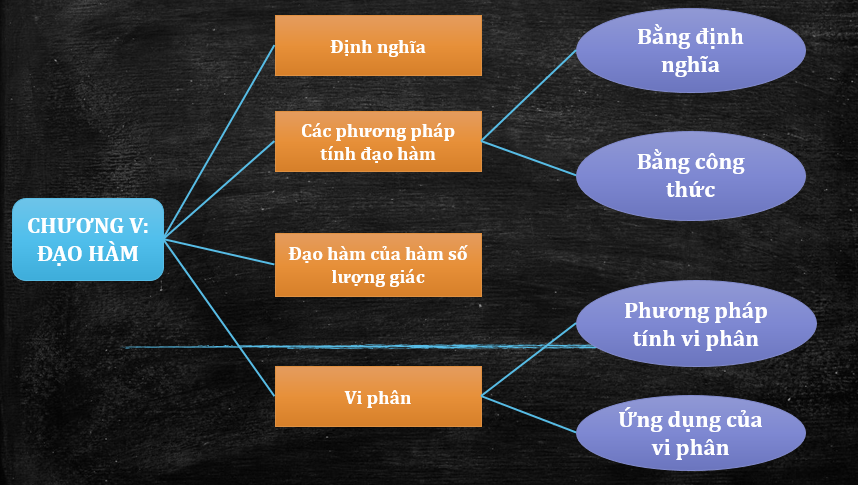
Hình 1: Hệ thống kiến thức chương đạo hàm
2. Các công thức tính đạo hàm
BẢNG 1: CÁC CÔNG THỨC ĐẠO HÀM LỚP 11
3. Bài tập Ôn tập
Ví dụ 1:
Tính đạo hàm các hàm số sau:
a) \(y = {x^3} - 2{x^2} + 3x + 4\)
b) \(y = \sin x - \cos x + \tan x\)
c) \(y = {x^4} + 2\sqrt x \)
d) \(y = \cot x - 3x + 2\)
Hướng dẫn:
a) \(y' = \left( {{x^3} - 2{x^2} + 3x + 4} \right)'\)
\(= 3{x^2} - 4x + 3\)
b) \(y' = \left( {\sin x - \cos x + \tan x} \right)' \)
\(= \cos x + \sin x + \frac{1}{{{{\cos }^2}x}}\)
c) \(y' = \left( {{x^4} + 2\sqrt x } \right)' = 4{x^3} + \frac{1}{{\sqrt x }}\)
d) \(y' = \left( {\cot x - 3x + 2} \right)' = - \frac{1}{{{{\sin }^2}x}} - 3\)
Ví dụ 2:
Tính đạo hàm các hàm số tại các điểm tương ứng
a) \(y = - {x^3} + 3{x^2} - 4x + 1\) tại \({x_0} = - 1\)
b) \(y = \sin 2x + \cos x\) tại \({x_0} = - \frac{\pi }{4}\)
c) \(y = \sqrt x - 2x\) tại \({x_0} = 2\)
Hướng dẫn:
a) \({y' = {{\left( { - {x^3} + 3{x^2} - 4x + 1} \right)}^\prime }}\)
\(\begin{array}{l}
= - 3{x^2} + 6x - 4\\
\Rightarrow y'\left( { - 1} \right) = - 3 - 6 - 4 = - 13
\end{array}\)
b)
\(\begin{array}{*{20}{l}}
{y' = {{\left( {\sin 2x + \cos x} \right)}^\prime } = 2\cos 2x - \sin x}\\
\begin{array}{l}
\Rightarrow y'\left( { - \frac{\pi }{4}} \right) = 2\cos \left( { - \frac{\pi }{2}} \right) - \sin \left( { - \frac{\pi }{4}} \right)\\
= \frac{{\sqrt 2 }}{2}
\end{array}
\end{array}\)
c) \({y' = {{\left( {\sqrt x - 2x} \right)}^\prime } = \frac{1}{{2\sqrt x }} - 2}\)
\({ \Rightarrow y'\left( 2 \right) = \frac{1}{{2\sqrt 2 }} - 2 = \frac{{1 - 4\sqrt 2 }}{{2\sqrt 2 }}}\)
Ví dụ 3:
Tính đạo hàm các hàm số
\(\begin{array}{l}
{\rm{a) }}\,y = \frac{{{x^2} + 3x - 1}}{{x + 1}}\\
{\rm{b) }}\,y = \sin \left( {2x + 1} \right) + \cos \left( {1 - x} \right)\\
{\rm{c) }}\,y = \sqrt {{x^2} + 4x + 1} \\
{\rm{d) }}\,y = \tan \left( {{x^2} + 2\sqrt x + 1} \right)
\end{array}\)
Hướng dẫn:
a) \({\rm{ }}y' = \left( {\frac{{{x^2} + 3x - 1}}{{x + 1}}} \right)' \)
\(= \frac{{\left( {2x + 3} \right)\left( {x + 1} \right) - \left( {{x^2} + 3x - 1} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2x + 4}}{{{{\left( {x + 1} \right)}^2}}}\)
b) \(y' = \left( {\sin \left( {2x + 1} \right) + \cos \left( {1 - x} \right)} \right)' \)
\(= 2\cos \left( {2x + 1} \right) + \sin \left( {1 - x} \right)\)
c) \(y' = \left( {\sqrt {{x^2} + 4x + 1} } \right)' = \frac{{2x + 4}}{{2\sqrt {{x^2} + 4x + 1} }} \)
\(= \frac{{x + 2}}{{\sqrt {{x^2} + 4x + 1} }}\)
d) \(y' = {\left( {\tan \left( {{x^2} + 2\sqrt x + 1} \right)} \right)^\prime }\)
\(\begin{array}{*{20}{l}}
{ = \frac{{{{\left( {{x^2} + 2\sqrt x + 1} \right)}^\prime }}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}} = \frac{{2x + \frac{1}{{\sqrt x }}}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}}}\\
{ = \frac{{2x\sqrt x + 1}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}}}
\end{array}\)
Ví dụ 4:
Chứng minh \(y' + 2{y^2} + 2 = 0\) với \(y = \cot 2x\)
Hướng dẫn:
Ta có \(y' = - \frac{2}{{{{\sin }^2}2x}}\)
Khi đó:
\(y' + 2{y^2} + 2 = - \frac{2}{{{{\sin }^2}2x}} + \frac{{2{{\cos }^2}2x}}{{{{\sin }^2}2x}} + 2 \)
\(= \frac{{ - 2 + 2\left( {{{\sin }^2}2x + {{\cos }^2}2x} \right)}}{{{{\sin }^2}2x}} = 0\) (đpcm)
1. Hệ thống kiến thức chương V Đại số và Giải tích 11
Hình 1: Hệ thống kiến thức chương đạo hàm
2. Các công thức tính đạo hàm
BẢNG 1: CÁC CÔNG THỨC ĐẠO HÀM LỚP 11
3. Bài tập Ôn tập
Ví dụ 1:
Tính đạo hàm các hàm số sau:
a) \(y = {x^3} - 2{x^2} + 3x + 4\)
b) \(y = \sin x - \cos x + \tan x\)
c) \(y = {x^4} + 2\sqrt x \)
d) \(y = \cot x - 3x + 2\)
Hướng dẫn:
a) \(y' = \left( {{x^3} - 2{x^2} + 3x + 4} \right)'\)
\(= 3{x^2} - 4x + 3\)
b) \(y' = \left( {\sin x - \cos x + \tan x} \right)' \)
\(= \cos x + \sin x + \frac{1}{{{{\cos }^2}x}}\)
c) \(y' = \left( {{x^4} + 2\sqrt x } \right)' = 4{x^3} + \frac{1}{{\sqrt x }}\)
d) \(y' = \left( {\cot x - 3x + 2} \right)' = - \frac{1}{{{{\sin }^2}x}} - 3\)
Ví dụ 2:
Tính đạo hàm các hàm số tại các điểm tương ứng
a) \(y = - {x^3} + 3{x^2} - 4x + 1\) tại \({x_0} = - 1\)
b) \(y = \sin 2x + \cos x\) tại \({x_0} = - \frac{\pi }{4}\)
c) \(y = \sqrt x - 2x\) tại \({x_0} = 2\)
Hướng dẫn:
a) \({y' = {{\left( { - {x^3} + 3{x^2} - 4x + 1} \right)}^\prime }}\)
\(\begin{array}{l}
= - 3{x^2} + 6x - 4\\
\Rightarrow y'\left( { - 1} \right) = - 3 - 6 - 4 = - 13
\end{array}\)
b)
\(\begin{array}{*{20}{l}}
{y' = {{\left( {\sin 2x + \cos x} \right)}^\prime } = 2\cos 2x - \sin x}\\
\begin{array}{l}
\Rightarrow y'\left( { - \frac{\pi }{4}} \right) = 2\cos \left( { - \frac{\pi }{2}} \right) - \sin \left( { - \frac{\pi }{4}} \right)\\
= \frac{{\sqrt 2 }}{2}
\end{array}
\end{array}\)
c) \({y' = {{\left( {\sqrt x - 2x} \right)}^\prime } = \frac{1}{{2\sqrt x }} - 2}\)
\({ \Rightarrow y'\left( 2 \right) = \frac{1}{{2\sqrt 2 }} - 2 = \frac{{1 - 4\sqrt 2 }}{{2\sqrt 2 }}}\)
Ví dụ 3:
Tính đạo hàm các hàm số
\(\begin{array}{l}
{\rm{a) }}\,y = \frac{{{x^2} + 3x - 1}}{{x + 1}}\\
{\rm{b) }}\,y = \sin \left( {2x + 1} \right) + \cos \left( {1 - x} \right)\\
{\rm{c) }}\,y = \sqrt {{x^2} + 4x + 1} \\
{\rm{d) }}\,y = \tan \left( {{x^2} + 2\sqrt x + 1} \right)
\end{array}\)
Hướng dẫn:
a) \({\rm{ }}y' = \left( {\frac{{{x^2} + 3x - 1}}{{x + 1}}} \right)' \)
\(= \frac{{\left( {2x + 3} \right)\left( {x + 1} \right) - \left( {{x^2} + 3x - 1} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2x + 4}}{{{{\left( {x + 1} \right)}^2}}}\)
b) \(y' = \left( {\sin \left( {2x + 1} \right) + \cos \left( {1 - x} \right)} \right)' \)
\(= 2\cos \left( {2x + 1} \right) + \sin \left( {1 - x} \right)\)
c) \(y' = \left( {\sqrt {{x^2} + 4x + 1} } \right)' = \frac{{2x + 4}}{{2\sqrt {{x^2} + 4x + 1} }} \)
\(= \frac{{x + 2}}{{\sqrt {{x^2} + 4x + 1} }}\)
d) \(y' = {\left( {\tan \left( {{x^2} + 2\sqrt x + 1} \right)} \right)^\prime }\)
\(\begin{array}{*{20}{l}}
{ = \frac{{{{\left( {{x^2} + 2\sqrt x + 1} \right)}^\prime }}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}} = \frac{{2x + \frac{1}{{\sqrt x }}}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}}}\\
{ = \frac{{2x\sqrt x + 1}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}}}
\end{array}\)
Ví dụ 4:
Chứng minh \(y' + 2{y^2} + 2 = 0\) với \(y = \cot 2x\)
Hướng dẫn:
Ta có \(y' = - \frac{2}{{{{\sin }^2}2x}}\)
Khi đó:
\(y' + 2{y^2} + 2 = - \frac{2}{{{{\sin }^2}2x}} + \frac{{2{{\cos }^2}2x}}{{{{\sin }^2}2x}} + 2 \)
\(= \frac{{ - 2 + 2\left( {{{\sin }^2}2x + {{\cos }^2}2x} \right)}}{{{{\sin }^2}2x}} = 0\) (đpcm)
.PNG)