Đề thi minh họa kỳ thi THPT Quốc gia năm 2017 môn Toán
Trong khi chờ đợi đề minh họa 2018 được công bố, thì mời các thầy cô cùng học sinh tham khảo đề minh họa THPT Quốc gia 2017 môn toán có kèm theo hướng dẫn giải chi tiết do TimDapAnsưu tầm và biên soạn. Không chỉ mang đến cho thầy cô, học sinh có thêm tài liệu tham khảo môn toán 12 bổ ích mà còn hỗ trợ các em trong việc tự đánh giá khả năng trước khi bước vào kì thi THPT Quốc gia 2018.
Bộ đề thi minh họa kỳ thi THPT Quốc gia năm 2017
Đề thi minh họa THPT Quốc gia năm 2017 môn Ngữ Văn
Đáp án - Đề thi chính thức THPT Quốc gia môn Toán năm 2016
Bộ đề thi thử THPT Quốc gia năm 2017 môn Toán - Số 1
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc
Đề thi minh họa môn Toán lần 3 năm 2017






Đáp án đề thi minh họa môn Toán THPT quốc gia 2017 lần 3


Tài liệu vẫn còn, mời bạn tải về
Đề thi minh họa môn Toán lần 2

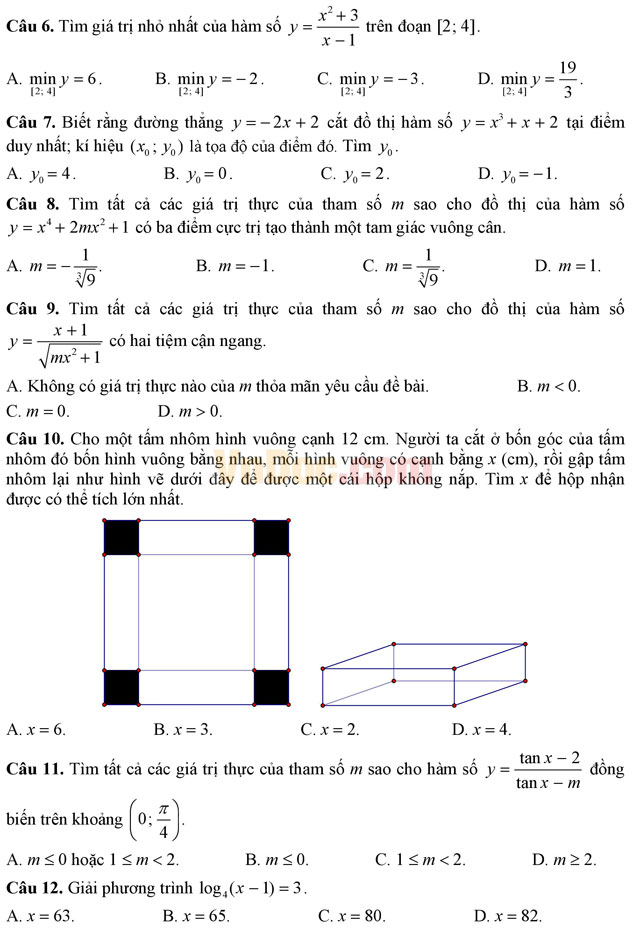






Đáp án đề thi minh họa kỳ thi THPT Quốc gia năm 2017 môn Toán
Dưới đây là gợi ý đáp án đề thi minh họa môn Toán 2017, mời các bạn cùng tham khảo.

Đề thi minh họa THPT Quốc Gia môn Toán năm 2015:
| BỘ GIÁO DỤC VÀ ĐÀO TẠO
| ĐỀ THI MINH HỌA - KỲ THI THPT QUỐC GIA NĂM 2015Môn: TOÁN Thời gian làm bài: 180 phút. |
Câu 1.(2,0 điểm) Cho hàm số:
| y = | 2x - 1 |
| x + 1 |
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp điểm có hoành độ x = 1

Câu 6. (1,0 điểm) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AC = 2a, góc ACB = 30o, Hình chiếu vuông góc H của đỉnh S trên mặt đáy là trung điểm của cạnh AC và SH a = √2 . Tính theo a thể tích khối chóp S.ABC và khoảng cách từ điểm C đến mặt phẳng (SAB).
Câu 7. (1,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác OAB có các đỉnh A và B thuộc đường thẳng ∆: 4x + 3y - 12 = 0 và điểm K(6; 6) là tâm đường tròn bàng tiếp góc O. Gọi C là điểm nằm trên ∆ sao cho AC = AO và các điểm C, B nằm khác phía nhau so với điểm A. Biết điểm C có hoành độ bằng 24/5 tìm tọa độ của các đỉnh A, B.
Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016
Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1
Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 2
Câu 8. (1,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2; 0; 0) và B(1; 1; -1). Viết phương trình mặt phẳng trung trực (P) của đoạn thẳng AB và phương trình mặt cầu tâm O, tiếp xúc với (P).
Câu 9. (0,5 điểm) Hai thí sinh A và B tham gia một buổi thi vấn đáp. Cán bộ hỏi thi đưa cho mỗi thí sinh một bộ câu hỏi thi gồm 10 câu hỏi khác nhau, được đựng trong 10 phong bì dán kín, có hình thức giống hệt nhau, mỗi phong bì đựng 1 câu hỏi; thí sinh chọn 3 phong bì trong số đó để xác định câu hỏi thi của mình. Biết rằng bộ 10 câu hỏi thi dành cho các thí sinh là như nhau, tính xác suất để 3 câu hỏi A chọn và 3 câu hỏi B chọn là giống nhau.
Câu 10. (1,0 điểm) Xét số thực x. Tìm giá trị nhỏ nhất của biểu thức sau:
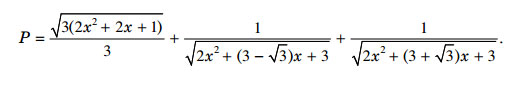
Đáp án đề thi minh họa THPT Quốc gia môn Toán
Đề thi minh họa và đáp án kỳ thi THPT Quốc gia môn Hóa năm 2016
Đề thi minh họa và đáp án kỳ thi THPT Quốc gia môn Ngữ văn năm 2016
Đề thi minh họa và đáp án kỳ thi THPT Quốc gia năm 2016 môn Vật Lý
Đề thi minh họa và đáp án kỳ thi THPT quốc gia môn Sinh học năm 2016
Đề thi minh họa và đáp án kỳ thi THPT quốc gia môn Tiếng Anh năm 2016
| BỘ GIÁO DỤC VÀ ĐÀO TẠO
| ĐÁP ÁN ĐỀ THI MINH HỌA - KỲ THI THPT QUỐC GIA NĂM 2015 Môn: TOÁN |
Câu 1 (2 điểm)
a, (1 điểm).
- Tập xác định: D = R \ {-1} .
- Giới hạn và tiệm cận:
![]()
Suy ra, đồ thị hàm số có một tiệm cận đứng là đường thẳng x = −1 và một tiệm cận ngang là đường thẳng y = 2.
- Sự biến thiên:
Chiều biến thiên y' = 3/(x + 1)2 > 0 với mọi x thuộc D suy ra hàm số đồng biến trên mỗi khoảng (−∞; −1) và (−1; +∞).
Cực trị: Hàm số đã cho không có cực trị.
Lưu ý: Cho phép thí sinh không nêu kết luận về cực trị của hàm số.
Bảng biến thiên:
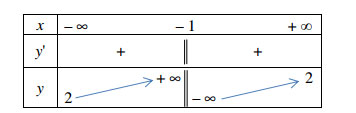
- Ta có đồ thị (C):
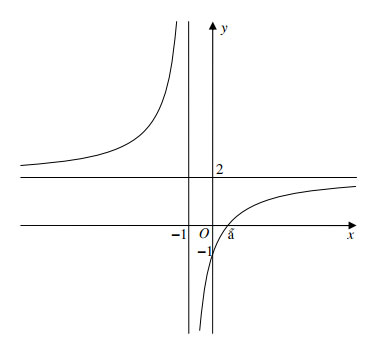
b, (1 điểm)
Tung độ yo của tiếp điểm là: yo = y(1) = 0,5.
Suy ra hệ số góc k của tiếp tuyến là: k = y'(1) = 0,75,
Do đó, phương trình của tiếp tuyến là: y = 3/4.(x-1) + 0,5 hay y = 3/4.(x - 1) - 1/4.
Câu 2.(1 điểm)
a, 0,5 điểm
Ta có A = tanα/(1 + tan²α) = tanα.cos²α = sinα.cosα = 0,6cosα (1)
cos²α = 1 - sin²α = 1 - 0,6² = 16/25 (2)
Vì α thuộc (π/2, π) nên cosα < 0. Do đó, từ (2) suy ra cosα = -0,8 (3)
Thế (3) vào (1) suy ra A = -12/25.
b, 0.5 điểm
Đặt z = a + bi, (a, b ∈ R); khi đó z ngang = a - bi. Do đó, kí hiệu (∗) là hệ thức cho trong đề bài, ta có:
(∗) ⇔ (1 + i)(a + bi) + (3 - i)(a - bi) = 2 - 6i.
⇔ (4a - 2b - 2) + (6 - 2b)i = 0.
- 4a - 2b - 2 = 0
- 6 - 2b = 0
Giải hệ được a = 2, b = 3. Do đó |z| = √(a² + b²) = √13.
Câu 3 (0,5 điểm)
- Điều kiện xác định: x > 0
- Với điều kiện đó, ký hiệu (2) là phương trình đã cho, ta có:
(2) ↔ log3(x+2) + log3x = 1 ↔ log3(x(x+2)) = log33 ↔ x² + 2x - 3 = 0 → x = 1 do điều kiện x > 0.
Câu 4 (1 điểm)

Mời các bạn cùng tham khảo các đề thi thử được Tìm Đáp Án sưu tầm và đăng tải:
| Tài liệu luyện thi đại học môn Toán | Tài liệu luyện thi đại học môn Hóa học | Tài liệu luyện thi đại học môn Vật lý | Tài liệu luyện thi đại học môn Sinh học |
| Tài liệu luyện thi đại học môn Ngữ văn | Tài liệu luyện thi đại học môn Lịch sử | Tài liệu luyện thi đại học môn Địa lý | Tài liệu luyện thi đại học môn Tiếng Anh |







