Đề kiểm tra 1 tiết môn Toán Chương 1 lớp 6

Đề kiểm tra 1 tiết môn Toán Chương 1 lớp 6 - Đề 2 bao gồm đáp án chi tiết cho từng dạng bài tập sẽ giúp các em học sinh ôn tập hệ thống lại kiến thức ôn tập chương trình học Toán 6 chương 1, ôn thi giữa 1 lớp 6 và cuối học kì 1 hiệu quả đạt kết quả cao. Mời các em cùng tham khảo chi tiết.

Đề bài kiểm tra 1 tiết môn Toán lớp 6

Bài 1. (3 điểm) Viết kết quả phép tính sau dưới dạng một lũy thừa:

a) 6²⁰¹⁰: 6¹⁰

b) (3⁸. 3¹⁶) : (3⁷ . 3¹⁴ )

c) (2²⁶: 2¹⁰) : (2¹⁸ : 2¹⁶)

d) 25³ : 125

Bài 2. (2 điểm) Tích của hai số là 2610. Nếu thêm 5 đơn vị vào một thừa số thì tích mới sẽ là 2900. Tìm hai số đó.

Bài 3. (2 điểm) Trong một phép chia số tự nhiên cho số tự nhiên, số bị chia là 236 và số dư là 15. Tìm số chia và thương.

Bài 4. (2 điểm )Tìm các thừa số và tích của các phép nhân sau :

Bài 5. (1 điểm) Tìm số tự nhiên nhỏ nhất, biết rằng khi chia số này cho 37 dư 1 và khi chia cho 39 dư 14.

Đáp án đề kiểm tra 45 phút môn Toán lớp 6

Bài 1.

a) 6²⁰¹⁰: 6¹⁰ = 6²⁰⁰⁰

b) (3⁸. 3¹⁶) : (3⁷ . 3¹⁴ ) = 3²⁴ : 3²¹ = 3³

c) (2²⁶: 2¹⁰ ) : (2¹⁸ : 2¹⁶) = 2¹⁶ : 2² = 2¹⁴

d) 25³ : 125= (25 . 25 . 25 ) : 5³ = 5⁶ : 5³ = 5³

Bài 2.

Tích mới hơn tích cũ là : 2900 – 2610 = 290

Tích mới hơn tích cũ 290 vì được thêm 5 lần thừa số kia

Thừa số kia là: 290 : 5 = 58

Thừa số này là: 2610 : 58 = 45

Bài 3.

Gọi a, b, q, r lần lượt là số bị chia, số chia, thương, số dư

Ta có: a = bq + r (b ≠ 0 và 0 < r < b)

236 = bq + 15

bq = 236 – 15 = 221

Mà : 221 = 221.1 = 13.17. Vì b > r = 15 nên ta chọn b = 221 hoặc b = 17

- Số chia là 221 thì thương là 1

- Số chia là 17 thì thương là 13

Bài 4.

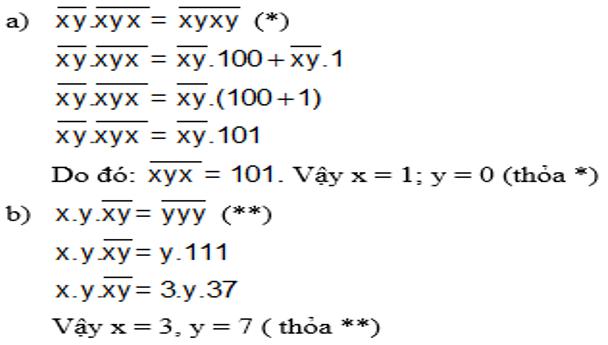
Bài 5.

Gọi số cần tìm là a. Gọi thương của phép chia số a lần lượt cho 37, 39 là h, k.

Ta có: a = 37h + 1 ; a = 39k + 14 và h ≠ k

37h + 1 = 39k + 14

37h – 37k = 2k + 13

37(h – k) = 2k + 13

Vì 2k + 13 là số tự nhiên lẻ nên 37 ( h – k ) là số tự nhiên lẻ

Do đó: h – k là số tự nhiên lẻ, suy ra h – k ≥ 1

a là số nhỏ nhất nên k nhỏ nhất, khi đó 2k nhỏ nhất

Do đó h – k nhỏ nhất nên h – k = 1

Ta có: 2k + 13 = 37 . 1 ⇒ 2k = 24 ⇒ k = 12. Khi đó: a = 39 . 12 + 14 = 482

Vậy a = 482