Công thức tích phân là một trong những phần trong thường xuyên xuất hiện trong đề thi đại học. Bài viết sau đây sẽ giúp các bạn ôn tập và củng cố các kiến thức cơ bản của tích phân như định nghĩa, phương pháp tính tích phân và bài tập minh họa. Mời các bạn cùng tham khảo nhằm ôn thi THPT quốc gia hiệu quả.
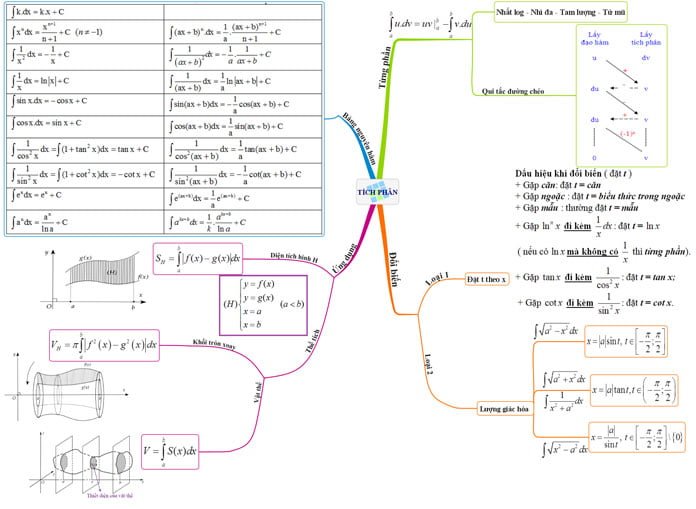
CÔNG THỨC TÍCH PHÂN
- Định nghĩa tích phân
- Tính chất của tích phân – Công thức tích phân
- Một số phương pháp tính tích phân
- Bài tập minh họa áp dụng công thức tích phân
Định nghĩa tích phân
Cho hàm f(x) liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu F(x) là một nguyên hàm của f(x) thì hiệu số F(b) − F(a) được gọi là tích phân của f(x) từ a đến b và ký hiệu là ![]() .
.
Tính chất của tích phân – Công thức tích phân
Cho các hàm số f(x), g(x) liên tục trên K và a, b, c là ba số thuộc K.
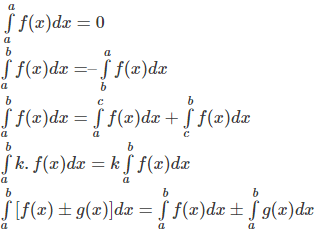
Một số phương pháp tính tích phân
Phương pháp đổi biến số
Công thức đổi biến số 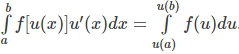 . Trong đó f(x) là hàm số liên tục và u(x) có đạo hàm liên tục trên khoảng J sao cho hàm hợp
. Trong đó f(x) là hàm số liên tục và u(x) có đạo hàm liên tục trên khoảng J sao cho hàm hợp xác định trên J; a, b ∈ J.
Các phương pháp đổi biến số thường gặp:
Cách 1: Đặt u = u(x) (u là một hàm theo x).
Cách 2: Đặt x = x(t) (x là một hàm theo t).
Phương pháp tích phân từng phần
Định lí:
Nếu u(x), v(x) là hai hàm số có đạo hàm liên tục trên khoảng K và a, b là hai số thuộc K thì ![]() .
.
Bài tập minh họa áp dụng công thức tích phân
Ví dụ 1:
Áp dụng công thức tính tích phân cơ bản, tính các tích phân sau:
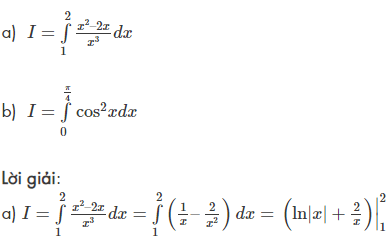
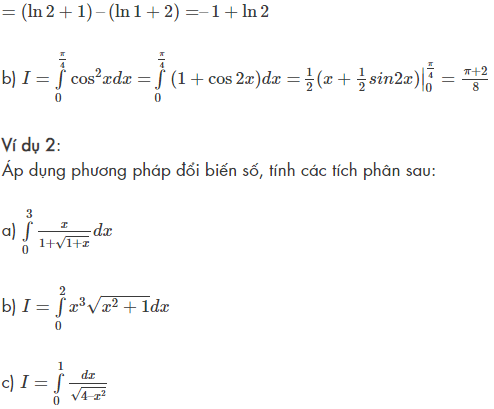
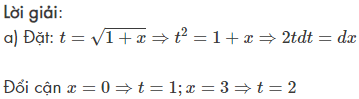
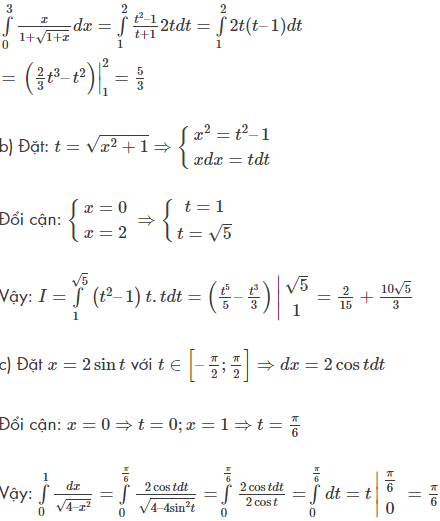
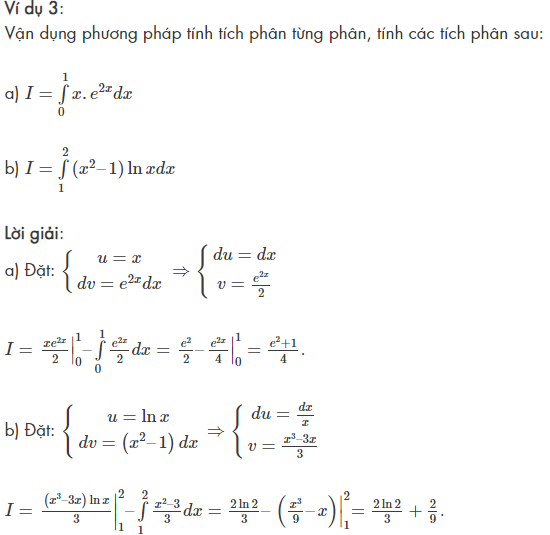
Các tài liệu liên quan:
- Bảng công thức Tích phân - Đạo hàm - Mũ - Logarit
- Ứng dụng của tích phân trong hình học (có lời giải chi tiết)
- Ôn thi Đại học môn Toán - Chuyên đề: Tích phân