Trả lời câu hỏi 2 Bài 9 trang 48 SGK Toán 7 Tập 2
Trả lời câu hỏi 2 Bài 9 trang 48 SGK Toán 7 Tập 2. Trong các số cho sau, với mỗi đa thức, số nào là nghiệm của đa thức?
Đề bài
Trong các số cho sau, với mỗi đa thức, số nào là nghiệm của đa thức?
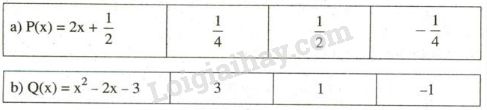
Phương pháp giải - Xem chi tiết
Nếu tại \(x = a\) đa thức \(P(x)\) có giá trị bằng \(0\) thì ta nói \(a\) là một nghiệm của đa thức \(P(x)\)
Lời giải chi tiết
a)
- Tại \(x = \dfrac{1}{4}\) ta có:
\(P\left( {\dfrac{1}{4}} \right) = 2.\dfrac{1}{4} + \dfrac{1}{2} = \dfrac{1}{2} + \dfrac{1}{2} = \dfrac{2}{2} \)\(\,= 1\)
Do đó \(x = \dfrac{1}{4}\) không là nghiệm của đa thức \(P(x)\).
- Tại \(x = \dfrac{1}{2}\) ta có:
\(P\left( {\dfrac{1}{2}} \right) = 2.\dfrac{1}{2} + \dfrac{1}{2} = \dfrac{2}{2} + \dfrac{1}{2} = \dfrac{3}{2}\)
Do đó \(x = \dfrac{1}{2}\) không là nghiệm của đa thức \(P(x)\)
- Tại \(x = - \dfrac{1}{4}\) ta có:
\(P\left( { - \dfrac{1}{4}} \right) = 2.\left( { - \dfrac{1}{4}} \right) + \dfrac{1}{2} \)\(\,= - \dfrac{2}{4} + \dfrac{1}{2} = - \dfrac{1}{2} + \dfrac{1}{2} = 0\)
Vậy \(x = - \dfrac{1}{4}\) là nghiệm của đa thức \(P(x)\).
b)
- Tại \(x=3\) ta có:
\(Q\left( 3 \right) = {3^2} - 2.3 - 3 = 9 - 6 - 3 = 0\)
Vậy \(x=3\) là nghiệm của đa thức \(Q(x)\).
- Tại \(x=1\) ta có:
\(Q\left( 1 \right) = {1^2} - 2.1 - 3 = 1 - 2 - 3 \)\(\,= - 4\)
Vậy \(x=1\) không là nghiệm của đa thức \(Q(x)\).
- Tại \(x=-1\) ta có:
\(Q\left( { - 1} \right) = {\left( { - 1} \right)^2} - 2.\left( { - 1} \right) - 3 \)\(\,= 1 + 2 - 3 = 0\)
Vậy \(x=-1\) là nghiệm của đa thức \(Q(x)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Trả lời câu hỏi 2 Bài 9 trang 48 SGK Toán 7 Tập 2 timdapan.com"







