Toán lớp 4 trang 64 - Bài 74: Phép nhân phân số - SGK Chân trời sáng tạo
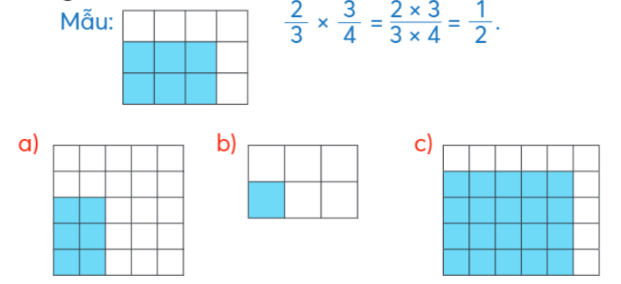
Viết theo mẫu, biết mỗi hình dưới đây được chia thành các phần bằng nhau. Viết các thừa số là số tự nhiên dưới dạng phân số rồi tính.
Câu 1
Viết theo mẫu, biết mỗi hình dưới đây được chia thành các phần bằng nhau.
Phương pháp giải:
- Viết phân số ứng với chiều rộng và chiều dài của hình chữ nhật được tô màu
- Nhân hai phân số: Muốn nhân hai phân số, ta nhân tử số với tử số, nhân mẫu số với mẫu số.
Lời giải chi tiết:
a) $\frac{2}{5} \times \frac{3}{5} = \frac{{2 \times 3}}{{5 \times 5}} = \frac{6}{{25}}$
b) $\frac{1}{2} \times \frac{1}{3} = \frac{{1 \times 1}}{{2 \times 3}} = \frac{1}{6}$
c) $\frac{4}{5} \times \frac{5}{6} = \frac{{4 \times 5}}{{5 \times 6}} = \frac{{20}}{{30}} = \frac{2}{3}$
Câu 1
Tính.
a) $\frac{1}{6} \times \frac{2}{3}$
b) $\frac{6}{5} \times \frac{3}{8}$
c) $\frac{4}{3} \times \frac{8}{9}$
d) $\frac{5}{{12}} \times \frac{{12}}{5}$
Phương pháp giải:
Muốn nhân hai phân số, ta nhân tử số với tử số, nhân mẫu số với mẫu số.
Lời giải chi tiết:
a) $\frac{1}{6} \times \frac{2}{3} = \frac{{1 \times 2}}{{6 \times 3}} = \frac{2}{{18}} = \frac{1}{9}$
b) $\frac{6}{5} \times \frac{3}{8} = \frac{{6 \times 3}}{{5 \times 8}} = \frac{{18}}{{40}} = \frac{9}{{20}}$
c) $\frac{4}{3} \times \frac{8}{9} = \frac{{4 \times 8}}{{3 \times 9}} = \frac{{32}}{{27}}$
d) $\frac{5}{{12}} \times \frac{{12}}{5} = \frac{{5 \times 12}}{{12 \times 5}} = \frac{{60}}{{60}} = 1$
Câu 2
Viết các thừa số là số tự nhiên dưới dạng phân số rồi tính.
a) $2 \times \frac{3}{{14}}$
b) $3 \times \frac{4}{9}$
c) $\frac{7}{{18}} \times 6$
d) $\frac{{19}}{{12}} \times 0$
Phương pháp giải:
- Mọi số tự nhiên đều viết được dưới dạng phân số có mẫu số là 1
- Muốn nhân hai phân số, ta nhân tử số với tử số, nhân mẫu số với mẫu số.
Lời giải chi tiết:
a) $2 \times \frac{3}{{14}} = \frac{2}{1} \times \frac{3}{{14}} = \frac{{2 \times 3}}{{1 \times 14}} = \frac{6}{{14}} = \frac{3}{7}$
b) $3 \times \frac{4}{9} = \frac{3}{1} \times \frac{4}{9} = \frac{{3 \times 4}}{{1 \times 9}} = \frac{{12}}{9} = \frac{4}{3}$
c) $\frac{7}{{18}} \times 6 = \frac{7}{{18}} \times \frac{6}{1} = \frac{{7 \times 6}}{{18 \times 1}} = \frac{{42}}{{18}} = \frac{7}{3}$
d) $\frac{{19}}{{12}} \times 0 = \frac{{19}}{{12}} \times \frac{0}{1} = \frac{{19 \times 0}}{{12 \times 1}} = 0$
Câu 3
Tính rồi so sánh kết quả.
$\frac{2}{7} \times 3$ và $\frac{2}{7} + \frac{2}{7} + \frac{2}{7}$
Phương pháp giải:
- Muốn nhân hai phân số, ta nhân tử số với tử số, nhân mẫu số với mẫu số.
- Muốn cộng các phân số cùng mẫu mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số
Lời giải chi tiết:
$\frac{2}{7} \times 3 = \frac{2}{7} \times \frac{3}{1} = \frac{6}{7}$
$\frac{2}{7} + \frac{2}{7} + \frac{2}{7} = \frac{{2 + 2 + 2}}{7} = \frac{6}{7}$
Vậy $\frac{2}{7} \times 3$ = $\frac{2}{7} + \frac{2}{7} + \frac{2}{7}$
Câu 4
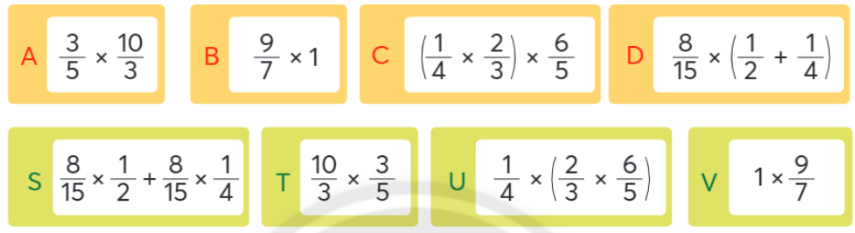
Các biểu thức nào có giá trị bằng nhau.
Nhận xét:
Phép nhân các phân số có tính chất giao hoán và kết hợp.
Một phân số nhân với 1 bằng chính phân số đó
Tính chất nhân một số với một tổng được áp dụng với các phân số.
Phương pháp giải:
Dựa vào tính chất của phân số để nối các biểu thức nào có giá trị bằng nhau:
- Phép nhân các phân số có tính chất giao hoán và kết hợp.
- Một phân số nhân với 1 bằng chính phân số đó
- Tính chất nhân một số với một tổng được áp dụng với các phân số.
Lời giải chi tiết:
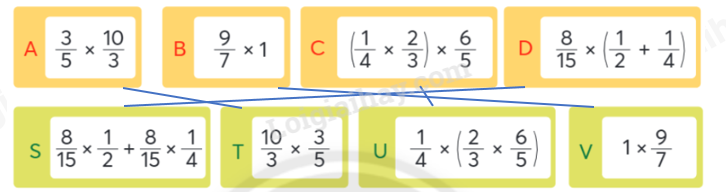
Câu 5
Tính.
a) $\frac{7}{9} \times \frac{{15}}{{28}} \times \frac{9}{7}$
b) $\frac{9}{{32}} \times \left( {\frac{2}{3} \times \frac{{14}}{{21}}} \right)$
Phương pháp giải:
Muốn nhân hai phân số, ta nhân tử số với tử số, nhân mẫu số với mẫu số.
Lời giải chi tiết:
a) $\frac{7}{9} \times \frac{{15}}{{28}} \times \frac{9}{7} = (\frac{7}{9} \times \frac{9}{7}) \times \frac{{15}}{{28}} = 1 \times \frac{{15}}{{28}} = \frac{{15}}{{28}}$
b) $\frac{9}{{32}} \times \left( {\frac{2}{3} \times \frac{{14}}{{21}}} \right) = \frac{9}{{32}} \times \left( {\frac{2}{3} \times \frac{2}{3}} \right) = \frac{9}{{32}} \times \frac{4}{9} = \frac{{36}}{{288}} = \frac{1}{8}$
Câu 6
Số?
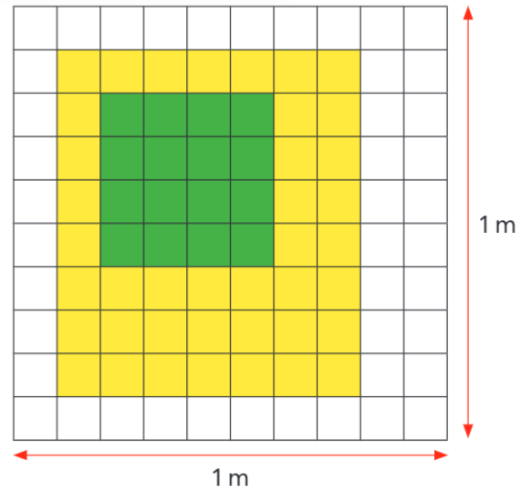
Hình vuông cạnh dài 1 m được chia thành các ô vuông nhỏ bằng nhau (xem hình). Phần màu vàng có diện tích là .......... m2.
Phương pháp giải:
- Tìm diện tích của hình vuông cạnh dài 1 m và diện tích của mỗi ô vuông nhỏ
- Đếm số ô vuông nhỏ được tô màu vàng rồi viết phân số chỉ diện tích của phần màu vàng
Lời giải chi tiết:
Diện tích của hình vuông cạnh dài 1 m là 1m2.
Hình vuông được chia thành 100 ô vuông nhỏ bằng nhau nên diện tích mỗi ô vuông nhỏ là $\frac{1}{{100}}$ m2
Có 40 ô vuông nhỏ được tô màu vàng.
Vậy phần màu vàng có diện tích là $\frac{{40}}{{100}} = \frac{2}{5}$ m2
Lý thuyết
Search google: "từ khóa + timdapan.com" Ví dụ: "Toán lớp 4 trang 64 - Bài 74: Phép nhân phân số - SGK Chân trời sáng tạo timdapan.com"