Thử tài bạn trang 76 Tài liệu dạy – học Toán 8 tập 2
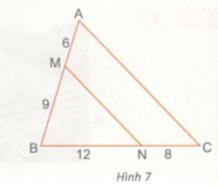
Giải bài tập Ở hình 7, cho biết BM = 9, MA = 6; BN = 12, NC = 8.
Đề bài
Ở hình 7, cho biết \(BM = 9, MA = 6; BN = 12, NC = 8.\)
a) Chứng minh : MN // AC.
b) Chứng minh tam giác BMN đồng dạng với tam giác BAC và viết dãy tỉ số đồng dạng.
Lời giải chi tiết
a) ∆ABC có \({{BM} \over {AM}} = {{BN} \over {CN}}\left( {vì\,{9 \over 6} = {{12} \over 8}} \right) \Rightarrow MN//AC\) (định lý Thales đảo)
b) Xét ∆BMN và ∆BAC có: \(\widehat {MBN} = \widehat {ABC},\widehat {BMN} = \widehat {BAC}\) (đồng vị và MN // AC),
\(\widehat {MNB} = \widehat {ACB}\) (đồng vị và MN // AC)
\({{MN} \over {AC}} = {{BM} \over {BA}} = {{BN} \over {BC}}\) (hệ quả của định lí Thales)
\(\eqalign{ & \Rightarrow \Delta BMN \sim \Delta BAC \cr & {{MN} \over {AC}} = {{BM} \over {BA}} = {{BN} \over {BC}} \cr} \)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Thử tài bạn trang 76 Tài liệu dạy – học Toán 8 tập 2 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Thử tài bạn trang 76 Tài liệu dạy – học Toán 8 tập 2 timdapan.com"