Lý thuyết Khoảng cách trong không gian - Toán 11 Chân trời sáng tạo
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
Nếu H là hình chiếu vuông góc của điểm M trên đường thẳng a thì độ dài đoạn MH được gọi là khoảng cách từ M đến đường thẳng a, kí hiệu d(M, a).
Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M, (P)).
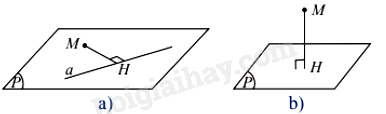
Quy ước:
- d(M, a) = 0 khi và chỉ khi M thuộc a;
- d(M, (P)) = 0 khi và chỉ khi M thuộc (P).
Nhận xét:
a) Lấy điểm N tùy ý trên đường thẳng a, ta luôn có \(d\left( {M,a} \right) \le MN\).
b) Lấy điểm N tùy ý trên mặt phẳng \(\left( P \right)\), ta luôn có \(d\left( {M,\left( P \right)} \right) \le MN\).
2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
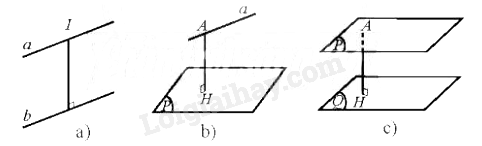
Khoảng cách giữa hai đường thẳng song song a và b là khoảng cách từ một điểm bất kì trên a đến b, kí hiệu d(a, b).
Khoảng cách giữa đường thẳng a đến mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P), kí hiệu d(a, (P)).
Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì trên (P) đến (Q), kí hiệu d((P), (Q)).
3. Khoảng cách giữa hai đường thẳng chéo nhau
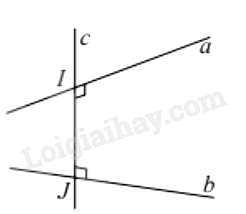
Đường thẳng c vừa vuông góc, vừa cắt hai đường thẳng chéo nhau a và b được gọi là đường vuông góc chung của a và b.
Nếu đường vuông góc chung của hai đường thẳng chéo nhau a và b cắt chúng lần lượt tại I và J thì đoạn IJ gọi là đoạn vuông góc chung của a và b.
Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó, kí hiệu d(a, b)
Chú ý:
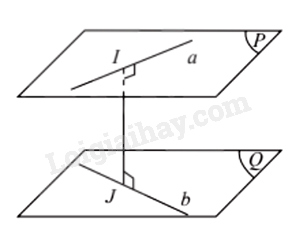
a) Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng khoảng cách giữa một trong hai đường thẳng đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
b) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
4. Công thức tính thể tích của khối chóp, khối lăng trụ, khối hộp
Thể tích khối hộp chữ nhật bằng ba kích thước:
\(V = abc\)
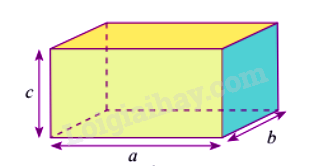
Thể tích khối chóp bằng một phần ba diện tích đáy nhân với chiều cao:
\(V = \frac{1}{3}S.h\)
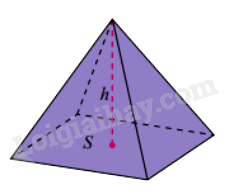
Thể tích khối chóp cụt đều có chiều cao h và diện tích hai đáy S, S’:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\)
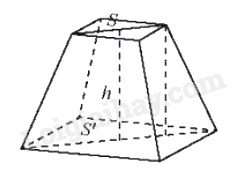
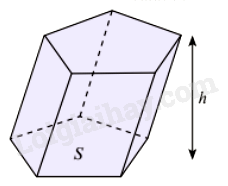
Thể tích khối lăng trụ bằng tích diện tích đáy và chiều cao:
\(V = Sh\)

Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Khoảng cách trong không gian - Toán 11 Chân trời sáng tạo timdapan.com"







