Bài 112 : Luyện tập chung

Bài 1

Viết chữ số thích hợp vào ô trống sao cho :

Phương pháp giải:

Áp dụng các dấu hiệu chia hết cho 2; 5; 9; 3:

- Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.

- Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.

- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.

- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.

- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.

Lời giải chi tiết:

Bài 2

Viết tiếp vào chỗ chấm:

Một đàn gà có \(\displaystyle35\) gà trống và \(\displaystyle51\) gà mái. Tổng số gà trong đàn là … con.

a) Phân số chỉ phần gà trống trong cả đàn gà là: ........

b) Phân số chỉ phần gà mái trong cả đàn gà là: .........

Phương pháp giải:

- Tìm tổng số gà trong đàn.

- Phân số chỉ phần gà trống (hoặc gà mái) trong cả đàn gà có tử số là số gà trống (hoặc gà mái) và mẫu số là tổng số gà của cả đàn.

Lời giải chi tiết:

 Một đàn gà có \(\displaystyle35\) gà trống và \(\displaystyle51\) gà mái. Tổng số gà trong đàn là \(\displaystyle86\) con.

a) Phân số chỉ phần gà trống trong cả đàn gà là: \(\displaystyle{{35} \over {86}}.\)

b) Phân số chỉ phần gà mái trong cả đàn gà là: \(\displaystyle{{51} \over {86}}.\)

Bài 3

Khoanh vào những phân số bằng \(\displaystyle{7 \over 9}\) :  

\(\displaystyle{{14} \over {27}}\;;\quad {{14} \over {18}}\;;\quad {{36} \over {28}}\;;\quad {{35} \over {45}}\)

Phương pháp giải:

Rút gọn các phân số đã cho thành phân số tối giản. Các phân số bằng phân số \(\displaystyle\dfrac{7}{9}\) thì rút gọn được thành phân số tối giản là \(\displaystyle\dfrac{7}{9}\).

Lời giải chi tiết:

 Rút gọn các phân số đã cho, ta có:

\(\displaystyle\dfrac{14}{18}=\dfrac{14:2}{18:2}=\dfrac{7}{9}\);                     \(\displaystyle\dfrac{36}{28}=\dfrac{36:4}{28:4}=\dfrac{9}{7}\)

\(\displaystyle\dfrac{35}{45}=\dfrac{35:5}{45:5}=\dfrac{7}{9}\).

\(\displaystyle\dfrac{14}{27}\) là phân số tối giản.

Vậy các phân số bằng \(\displaystyle\dfrac{7}{9}\) là: \(\displaystyle\dfrac{14}{18};\dfrac{35}{45}\).

Bài 4

Các phân số \(\displaystyle{{35} \over {63}};{{35} \over {58}};{{24} \over {54}}\) viết theo thứ tự từ lớn đến bé.

Phương pháp giải:

- So sánh các phân số rồi sắp xếp theo thứ tự từ lớn đến bé.

- Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì lớn hơn.

- Trong hai phân số có cùng mẫu số, phân số nào có tử số bé hơn thì bé hơn.

Lời giải chi tiết:

 Hai phân số \(\displaystyle{{35} \over {63}};{{35} \over {58}}\) có tử số bằng nhau.

Vì \(\displaystyle63 > 58\) nên \(\displaystyle{{35} \over {63}} < {{35} \over {58}}\,\,\left( 1 \right)\)

Mặt khác ta lại có :

\(\displaystyle\dfrac{35}{63}=\dfrac{35:7}{63:7}=\dfrac{5}{9}\);             \(\displaystyle\dfrac{24}{54}=\dfrac{24:6}{54:6}=\dfrac{4}{9}\)

Mà \(\displaystyle{5 \over 9} > {4 \over 9}\). Vậy \(\displaystyle{{35} \over {63}} > {{24} \over {54}}\,\,\left( 2 \right)\)

Từ \((1)\) và \((2)\) ta có thể viết như sau: \(\displaystyle{{35} \over {58}} > {{35} \over {63}} > {{24} \over {54}}\)

Vậy các phân số viết theo thứ tự từ lớn đến bé là: \(\displaystyle{{35} \over {58}};{{35} \over {63}};{{24} \over {54}}.\)

Bài 5

Viết tiếp vào chố chấm :

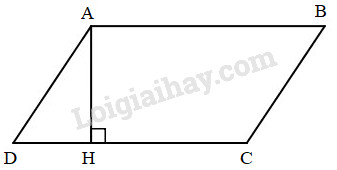
a) Đo độ dài đáy và chiều cao của hình bình hành ABCD được:

    Độ dài đáy DC : …...............

    Chiều cao AH là : …...............

b) Diện tích hình bình hành ABCD là : …...............

Phương pháp giải:

- Dùng thước kẻ để đo độ dài của cạnh đáy Dc và chiều cao AH.

- Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao.

Lời giải chi tiết:

 a) Đo độ dài đáy và chiều cao của hình bình hành ABCD được: 

   Độ dài đáy DC: 5cm

   Chiều cao AH là: 3cm

b) Diện tích hình bình hành ABCD là: 3 × 5 = 15cm².