Phần câu hỏi bài 4 trang 47 Vở bài tập toán 8 tập 2

Câu 9.

Khoanh tròn vào chữ cái trước khẳng định đúng. Bất phương trình \(x+1<2\) tương đương với các bất phương trình:

\(\begin{array}{l}
(A)\,x \le 1\\
(B)\,x + 2 < 4\\
(C)\,x > 1\\
(D)\,x + 2 < 3
\end{array}\) 

Phương pháp giải:

Sử dụng: Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.

Giải chi tiết:

Ta có:

\(\begin{array}{l}
x + 1 < 2\\
\Leftrightarrow x < 2 - 1\\
\Leftrightarrow x < 1
\end{array}\)

Vậy tập nghiệm của bất phương trình \(x+1<2\) là \(x<1\). 

\(\begin{array}{l}
x + 2 < 4\\
\Leftrightarrow x < 4 - 2\\
\Leftrightarrow x < 2
\end{array}\)

Vậy tập nghiệm của bất phương trình \(x+2<4\) là \(x<2\).

\(\begin{array}{l}
x + 2 < 3\\
\Leftrightarrow x < 3 - 2\\
\Leftrightarrow x < 1
\end{array}\)

Vậy tập nghiệm của bất phương trình \(x+2<3\) là \(x<1\).

Do đó phương trình \(x+1<2\) và \(x+2<3\) có cùng tập nghiệm là \(x<1\) nên hai phương trình này tương đương.

Chọn D.

Câu 10.

Khoanh tròn vào chữ cái trước khẳng định đúng. Bất phương trình bậc nhất \(2x+3<1\) có tập nghiệm biểu diễn bởi hình vẽ sau:

Phương pháp giải:

Tìm tập nghiệm của bất phương trình \(2x+3<1\) từ đó chọn hình vẽ biểu diễn tập nghiệm đó.

Giải chi tiết:

\(\begin{array}{l}
2x + 3 < 1\\
\Leftrightarrow 2x < 1 - 3\\
\Leftrightarrow 2x < - 2\\
\Leftrightarrow x < \left( { - 2} \right):2\\ 
\Leftrightarrow x < - 1
\end{array}\)

Biểu diễn tập nghiệm trên trục số như sau:

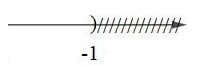
Chọn B.