Phần câu hỏi bài 11 trang 32, 33 Vở bài tập toán 8 tập 1

Câu 33.

Nối một biểu thức ở cột bên trái với một biểu thức ở cột bên phải để được đẳng thức đúng.

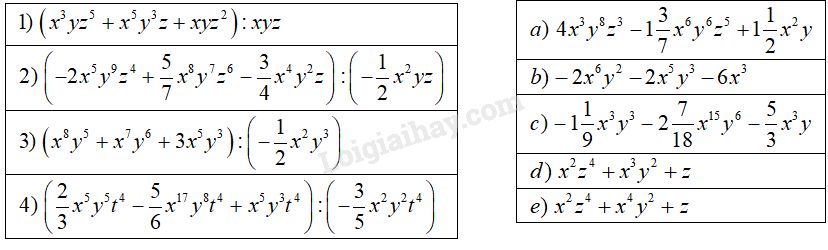
Phương pháp giải:

Muốn chia đa thức \(A\) cho đơn thức \(B\) (trường hợp các hạng tử của đa thức \(A\) đều chia hết cho đơn thức \(B\)), ta chia mỗi hạng tử của \(A\) cho \(B\) rồi cộng các kết quả với nhau.

Lời giải chi tiết:

\(1)\,\,\left( {{x^3}y{z^5} + {x^5}{y^3}z + xy{z^2}} \right):xyz\)

\( = \left( {{x^3}y{z^5}} \right):xyz + \left( {{x^5}{y^3}z} \right):xyz\)\( + \left( {xy{z^2}} \right):xyz\)

\( = {x^2}{z^4} + {x^4}{y^2} + z\)

\(2)\,\,\left( { - 2{x^5}{y^9}{z^4} + \dfrac{5}{7}{x^8}{y^7}{z^6} - \dfrac{3}{4}{x^4}{y^2}z} \right)\)\(:\left( { - \dfrac{1}{2}{x^2}yz} \right)\)

\( = \left( { - 2{x^5}{y^9}{z^4}} \right):\left( { - \dfrac{1}{2}{x^2}yz} \right) \)\(+ \left( {\dfrac{5}{7}{x^8}{y^7}{z^6}} \right):\left( { - \dfrac{1}{2}{x^2}yz} \right) \)\(+ \left( { - \dfrac{3}{4}{x^4}{y^2}z} \right):\left( { - \dfrac{1}{2}{x^2}yz} \right)\) 

\( = 4{x^3}{y^8}{z^3} - \dfrac{{10}}{7}{x^6}{y^6}{z^5} + \dfrac{3}{2}{x^2}y\)

\( = 4{x^3}{y^8}{z^3} - 1\dfrac{3}{7}{x^6}{y^6}{z^5} + 1\dfrac{1}{2}{x^2}y\)

\(3)\,\,\left( {{x^8}{y^5} + {x^7}{y^6} + 3{x^5}{y^3}} \right)\)\(:\left( { - \dfrac{1}{2}{x^2}{y^3}} \right)\)

\( = \left( {{x^8}{y^5}} \right):\left( { - \dfrac{1}{2}{x^2}{y^3}} \right) \)\(+ \left( {{x^7}{y^6}} \right):\left( { - \dfrac{1}{2}{x^2}{y^3}} \right)\) \( + \left( {3{x^5}{y^3}} \right):\left( { - \dfrac{1}{2}{x^2}{y^3}} \right)\)

\( =  - 2{x^6}{y^2} - 2{x^5}{y^3} - 6{x^3}\)

\(4)\,\,\left( {\,\,\dfrac{2}{3}{x^5}{y^5}{t^4} - \dfrac{5}{6}{x^{17}}{y^8}{t^4} + {x^5}{y^3}{t^4}} \right)\) \(:\left( { - \dfrac{3}{5}{x^2}{y^2}{t^4}} \right)\)

\( = \left( {\,\dfrac{2}{3}{x^5}{y^5}{t^4}} \right):\left( { - \dfrac{3}{5}{x^2}{y^2}{t^4}} \right)\) \( + \left( { - \dfrac{5}{6}{x^{17}}{y^8}{t^4}} \right):\left( { - \dfrac{3}{5}{x^2}{y^2}{t^4}} \right)\) \( + \left( {{x^5}{y^3}{t^4}} \right):\left( { - \dfrac{3}{5}{x^2}{y^2}{t^4}} \right)\)

\( = \dfrac{{ - 10}}{9}{x^3}{y^3} + \dfrac{{25}}{{18}}{x^{15}}{y^6} - \dfrac{5}{3}{x^3}y\)

\( =  - 1\dfrac{1}{9}{x^3}{y^3} + 1\dfrac{7}{{18}}{x^{15}}{y^6} - \dfrac{5}{3}{x^3}y\)

Ta nối như sau:

1 – e; 2 – a; 3 – b.

4 không có đáp án nào phù hợp. 

Chú ý:

Đề bài trong sách thiếu dấu ngoặc của đa thức bị chia.

Câu 34.

Khoanh tròn vào chữ cái trước kết quả đúng

Đa thức \(5{a^2}{b^3} + {a^5}{b^3} + {a^7}{b^2}\)  chia hết cho đơn thức \({a^{n - 1}}{b^n}\)  khi

\((A)\,\,n = 1\)  hoặc \(n = 2\)

\((B)\,\,n \le 3\)

\((C)\,\,n = 0\)

\((D)\,\,n \ge 1\) 

Phương pháp giải:

- Muốn chia đa thức \(A\) cho đơn thức \(B\) (trường hợp các hạng tử của đa thức \(A\) đều chia hết cho đơn thức \(B\)), ta chia mỗi hạng tử của \(A\) cho \(B\) rồi cộng các kết quả với nhau.

- Đa thức \(A\) chia hết cho đơn thức \(B\) nếu từng hạng tử của đa thức \(A\) chia hết cho đơn thức \(B.\)

- Quy tắc chia hai lũy thừa cùng cơ số: \({x^m}:{x^n} = {x^{m - n}}\)  với \(m, n\) là số tự nhiên, \(m \ge n\) 

Lời giải chi tiết:

\(\left( {5{a^2}{b^3} + {a^5}{b^3} + {a^7}{b^2}} \right):{a^{n - 1}}{b^n}\)

\( = \left( {5{a^2}{b^3}:{a^{n - 1}}{b^n}} \right) \)\(+ \left( {{a^5}{b^3}:{a^{n - 1}}{b^n}} \right) \)\(+ \left( {{a^7}{b^2}:{a^{n - 1}}{b^n}} \right)\)

\( = 5{a^{2 - \left( {n - 1} \right)}}.{b^{3 - n}} \)\(+ {a^{5 - \left( {n - 1} \right)}}.{b^{3 - n}} \)\(+ {a^{7 - \left( {n - 1} \right)}}.{b^{2 - n}}\)

\(= 5{a^{2 - n + 1}}{b^{3 - n}} + {a^{5 - n + 1}}{b^{3 - n}} \)\(+ {a^{7 - n + 1}}{b^{2 - n}}\)

\( = 5{a^{3 - n}}{b^{3 - n}} + {a^{6 - n}}{b^{3 - n}} \)\(+ {a^{8 - n}}{b^{2 - n}}\)

Để đa thức \(5{a^2}{b^3} + {a^5}{b^3} + {a^7}{b^2}\)  chia hết cho đơn thức \({a^{n - 1}}{b^n}\) thì

\(\left\{ \begin{array}{l}3 - n \ge 0\\6 - n \ge 0\\8 - n \ge 0\\2 - n \ge 0\\n - 1 \ge 0\\n \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}n \le 3\\n \le 6\\n \le 8\\n \le 2\\n \ge 1\\n \ge 0\end{array} \right. \)\(\Leftrightarrow 1 \le n \le 2\)

Mà \(n \in N\)  nên  \(n = 1\)  hoặc \(n = 2\) .  

Chọn A.

Câu 35.

Điền vào chỗ … để được đẳng thức đúng

\(\left( {2{x^3}{y^7} - \dfrac{1}{6}{x^7}{y^5} + {x^4}{y^3}} \right)\)\(:\left( { - \dfrac{1}{5}x{y^2}} \right) \)\(= ...{x^2}{y^5} + \dfrac{{...}}{6}{x^6}{y^{...}} - ...{x^3}...\)

\(2)\,\,\left( {12{x^n}{y^m}{t^p} + \dfrac{2}{3}{x^{n + 3}}{y^{m + 1}} - {x^{n + 4}}{y^m}{t^{p + 3}}} \right)\)\(:{x^{n - 5}}{y^{m - 2}}{t^{p - 1}}\)

\( = 12{x^5}{y^2}t + \dfrac{2}{3}... - ...{t^4}.\) 

Phương pháp giải:

- Muốn chia đa thức \(A\) cho đơn thức \(B\) (trường hợp các hạng tử của đa thức \(A\) đều chia hết cho đơn thức \(B\)), ta chia mỗi hạng tử của \(A\) cho \(B\) rồi cộng các kết quả với nhau.

Lời giải chi tiết:

\(1)\,\,\left( {2{x^3}{y^7} - \dfrac{1}{6}{x^7}{y^5} + {x^4}{y^3}} \right)\)\(:\left( { - \dfrac{1}{5}x{y^2}} \right)\)

\( = \left( {2{x^3}{y^7}} \right):\left( { - \dfrac{1}{5}x{y^2}} \right) \)\(+ \left( { - \dfrac{1}{6}{x^7}{y^5}} \right):\left( { - \dfrac{1}{5}x{y^2}} \right) \)\(+ \left( {{x^4}{y^3}} \right):\left( { - \dfrac{1}{5}x{y^2}} \right)\)

\( =  - 10{x^2}{y^5} + \dfrac{5}{6}{x^6}{y^3} - 5{x^3}y\)

\(2)\,\,\left( {12{x^n}{y^m}{t^p} + \dfrac{2}{3}{x^{n + 3}}{y^{m + 1}} - {x^{n + 4}}{y^m}{t^{p + 3}}} \right)\)\(:{x^{n - 5}}{y^{m - 2}}{t^{p - 1}}\)

\( = \left( {12{x^n}{y^m}{t^p}:{x^{n - 5}}{y^{m - 2}}{t^{p - 1}}} \right) \)\(+ \left( {\dfrac{2}{3}{x^{n + 3}}{y^{m + 1}}:{x^{n - 5}}{y^{m - 2}}{t^{p - 1}}} \right) \)\(+ \left( { - {x^{n + 4}}{y^m}{t^{p + 3}}:{x^{n - 5}}{y^{m - 2}}{t^{p - 1}}} \right)\)

\( = 12{x^5}{y^2}t + \dfrac{2}{3}{x^8}{y^3}{t^{1 - p}} \)\(- {x^9}{y^2}{t^4}.\)

Chú ý:

\(1)\;{t^{p - 1}} = {t^0}:{t^{p - 1}} \)\(= {t^{0 - \left( {p - 1} \right)}} \)\(= {t^{ - p + 1}} = {t^{1 - p}}\)