Giải mục 3 trang 76, 77 SGK Toán 9 tập 2 - Cánh diều
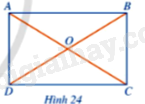
Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 76 SGK Toán 9 Cánh diều
Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?
Phương pháp giải:
Áp dụng tính chất: Hình chữ nhật có 2 đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường” để chứng minh AO = CO = OB = OD = R.
Lời giải chi tiết:
Do ABCD là hình chữ nhật nên 2 đường chéo cắt nhau tại trung điểm O của mỗi đường, do đó AO = CO= \(\frac{1}{2}AC\) và OB = OD = \(\frac{1}{2}BD\). Mà AC = BD (tính chất hình chữ nhật)
Suy ra AO = CO = OB = OD = R.
Vậy các điểm A, B, C, D thuộc (O; R).
LT3
Trả lời câu hỏi Luyện tập 3 trang 77 SGK Toán 9 Cánh diều
Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 8cm và 6cm. Hình chữ nhật được tô màu xanh còn phần khác của logo được tô màu đỏ. Tính diện tích phần được tô màu đỏ.
Phương pháp giải:
Diện tích tô màu đỏ = diện tích hình tròn – diện tích hình chữ nhật.
Lời giải chi tiết:
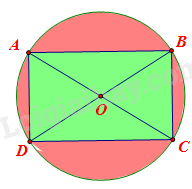
Giả sử ta có hình chữ nhật ABCD nội tiếp đường tròn tâm (O).
Suy ra bán kính đường tròn là OC, đường kính AC.
Hình chữ nhật ABCD có chiều dài AB = 8cm, chiều rộng BC = 6cm. Áp dụng định lý Pytago trong tam giác vuông ABC có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{8^2} + {6^2}} = 10cm.\)
Do đó \(R = OC = \frac{{AC}}{2} = \frac{{10}}{2} = 5cm.\)
Diện tích hình tròn là: \(\pi {R^2} = \pi {.5^2} = 25\pi (c{m^2}).\)
Diện tích hình chữ nhật là: \(8.6 = 48(c{m^2}).\)
Diện tích phần tô màu đỏ là: \(25\pi - 48 \approx 30,5(c{m^2})\) (với \(\pi \approx 3,14\)).
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 77 SGK Toán 9 Cánh diều
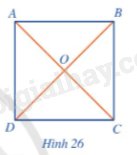
Cho hình vuông ABCD, AC cắt BD tại (O) (Hình 26).
a) Mỗi đường chéo của hình vuông ABCD có phải là đường kính của đường tròn ngoại tiếp hình vuông đó hay không?
b) Cho biết AB = a, tính OA theo a.
Phương pháp giải:
a) Mỗi hình vuông là một hình chữ nhật.
b) Áp dụng định lý Pytago trong tam giác OAB.
Lời giải chi tiết:
a) Vì hình vuông cũng là một hình chữ nhật nên mỗi đường chéo của hình vuông cũng là đường kính của đường tròn ngoại tiếp hình vuông đó.
b) Vì ABCD là hình vuông nên \(AC \bot BD\) hay \(\widehat {AOB} = 90^\circ \) và OA = OB.
Xét tam giác OAB vuông tại O, ta có:
\(\begin{array}{l}O{A^2} + O{B^2} = A{B^2}\\2O{A^2} = {a^2}\\OA = \frac{{\sqrt 2 a}}{2}.\end{array}\)
Vậy \(OA = \frac{{\sqrt 2 a}}{2}.\)
LT4
Trả lời câu hỏi Luyện tập 4 trang 77 SGK Toán 9 Cánh diều
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó.
Phương pháp giải:
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó là: chu vi hình vuông : chu vi đường tròn.
Lời giải chi tiết:
Giả sử hình vuông có cạnh là a, thì bán kính đường tròn ngoại tiếp hình vuông đó là \(\frac{{\sqrt 2 a}}{2}.\)
Chu vi hình vuông là 4a, chu vi của đường tròn ngoại tiếp là \(2\frac{{\sqrt 2 a}}{2}\pi = \sqrt 2 a\pi .\)
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó là: \(\frac{{4a}}{{\sqrt 2 a\pi }} = \frac{{2\sqrt 2 }}{\pi }.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 3 trang 76, 77 SGK Toán 9 tập 2 - Cánh diều timdapan.com"







