Giải mục 3 trang 43 SGK Toán 8 tập 1 - Kết nối tri thức

Luyện tập 3

Phân tích đa thức \(2{x^2} - 4xy + 2y - x\) thành nhân tử.

Phương pháp giải:

Sử dụng cách nhóm hạng tử

Lời giải chi tiết:

\(2{x^2} - 4xy + 2y - x = \left( {2{x^2} - 4xy} \right) + \left( {2y - x} \right) = 2x\left( {x - 2y} \right) - \left( {x - 2y} \right) = \left( {x - 2y} \right)\left( {2x - 1} \right)\)

Tranh luận

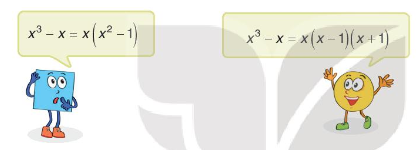
Phân tích đa thức \({x^3} - x\) thành nhân tử.

Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.

Phương pháp giải:

Kết hợp phương pháp đặt nhân tử chung và sử dụng hằng đẳng thức.

Lời giải chi tiết:

\({x^3} - x = x\left( {{x^2} - 1} \right) = x\left( {x - 1} \right)\left( {x + 1} \right)\)

Bạn Tròn có kết quả đúng, bạn Vuông chưa phân tích triệt để.

Vận dụng 2

Tính nhanh giá trị của biểu thức

\(A = {x^2} + 2y - 2x - xy\) tại \(x = 2022,y = 2020\)

Phương pháp giải:

Phân tích đa thức thành nhân tử bằng cách nhóm hạng tử rồi thay các giá trị của x, y vào biểu thức.

Lời giải chi tiết:

\(A = {x^2} + 2y - 2x - xy \\= \left( {{x^2} - 2x} \right) + \left( {2y - xy} \right) \\= x\left( {x - 2} \right) + y\left( {2 - x} \right) \\= x\left( {x - 2} \right) - y\left( {x - 2} \right) \\= (x-y)(x-2) \)

Thay \(x = 2022,y = 2020\) vào A ta được:

\(A = (2022 - 2020)(2022-2) = 2.2020 = 4040\)