Giải mục 2 trang 68, 69 SGK Toán 8 tập 2– Chân trời sáng tạo

Hoạt động 2

Cho tam giác \(DEF\) và tam giác \(ABC\) có \(DE = \frac{1}{3}AB,DF = \frac{1}{3}AC,\widehat D = \widehat A\) (Hình 5). Trên tia \(AB\), lấy điểm \(M\) sao cho \(AM = DE\). Qua \(M\) kẻ \(MN//BC\left( {N \in AC} \right)\).

a) So sánh \(\frac{{AM}}{{AB}}\) và \(\frac{{AN}}{{AC}}\)

b) So sánh \(AN\) với \(DF\).

c) Tam giác \(AMN\) có đồng dạng với tam giác \(ABC\) không?

d) Dự đoán sự đồng dạng của hai tam giác \(DEF\) và \(ABC\).

Phương pháp giải:

- Sử dụng định lí Thales.

- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Lời giải chi tiết:

a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).

b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).

Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).

c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)

d) Dự đoán  hai tam giác \(DEF\) và \(ABC\) đồng dạng.

Thực hành 2

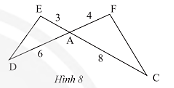
Cho tam giác \(ADE\) và tam giác \(ACF\) có các kích thước như trong Hình 8. Chứng minh rằng \(\Delta ADE\backsim\Delta ACF\).

Phương pháp giải:

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.

Lời giải chi tiết:

Ta có: \(\frac{{AE}}{{AF}} = \frac{3}{4};\frac{{AD}}{{AC}} = \frac{6}{8} = \frac{3}{4}\);

Xét \(\Delta ADE\) và \(\Delta ACF\) có:

\(\frac{{AE}}{{AF}} = \frac{{AD}}{{AC}} = \frac{3}{4}\)

\(\widehat {EAD} = \widehat {FAC}\) (hai góc đối đỉnh)

Do đó, \(\Delta ADE\backsim\Delta ACF\)(c.g.c)