Giải mục 2 trang 60, 61, 62 SGK Toán 11 tập 2 - Chân trời sáng tạo
Nêu nhận xét về vị trí tương đối của:
Hoạt động 4
Nêu nhận xét về vị trí tương đối của:
a) Hai thân cây cùng mọc vuông góc với mặt đất.
b) Mặt bàn và mặt đất cùng vuông góc với chân bàn.
c) Thanh xà ngang nằm trên trần nhà và mặt sàn nhà cùng vuông góc với cột nhà.

Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Hai thân cây cùng mọc vuông góc với mặt đất song song với nhau.
b) Mặt bàn và mặt đất song song với nhau.
c) Thanh xà ngang nằm trên trần nhà và mặt sàn nhà song song với nhau.
Thực hành 2
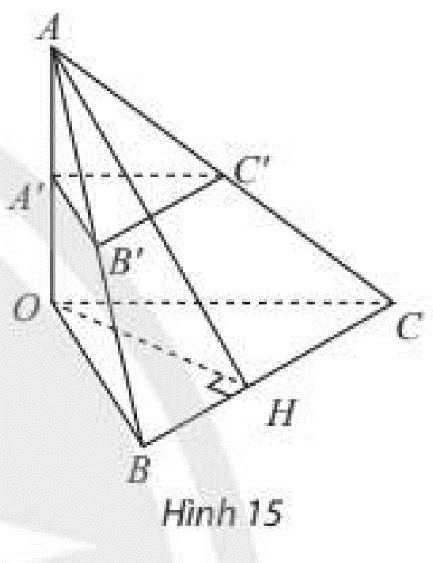
Cho tứ diện \(OABC\) có \(OA\) vuông góc với mặt phẳng \(\left( {OBC} \right)\) và có \(A',B',C'\) lần lượt là trung điểm của \(OA,AB,AC\). Vẽ \(OH\) là đường cao của tam giác \(OBC\). Chứng minh rằng:
a) \(OA \bot \left( {A'B'C'} \right)\);
b) \(B'C' \bot \left( {OAH} \right)\).
Phương pháp giải:
Sử dụng các định lí:
‒ Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
‒ Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Lời giải chi tiết:
a) Ta có: \(A'\) là trung điểm của \(OA\)
\(B'\) là trung điểm của \(AB\)
\( \Rightarrow A'B'\) là đường trung bình của \(\Delta OAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel OB\\OB \subset \left( {OBC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {OBC} \right)\)
\(B'\) là trung điểm của \(AB\)
\(C'\) là trung điểm của \(AC\)
\( \Rightarrow B'C'\) là đường trung bình của \(\Delta ABC\)
\(\left. \begin{array}{l} \Rightarrow B'C'\parallel BC\\BC \subset \left( {OBC} \right)\end{array} \right\} \Rightarrow B'C'\parallel \left( {OBC} \right)\)
\(\left. \begin{array}{l}A'B'\parallel \left( {OBC} \right)\\B'C'\parallel \left( {OBC} \right)\\A'B',B'C' \subset \left( {A'B'C'} \right)\end{array} \right\} \Rightarrow \left( {A'B'C'} \right)\parallel \left( {OBC} \right)\)
Lại có \(OA \bot \left( {OBC} \right)\)
Vậy \(OA \bot \left( {A'B'C'} \right)\).
b) Ta có:
\(\left. \begin{array}{l}OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC\\OH \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {OAH} \right)\)
Lại có \(BC\parallel B'C'\)
Vậy \(B'C' \bot \left( {OAH} \right)\).
Thực hành 3
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông với \(AB\) là cạnh góc vuông và có cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Cho \(M,N,P,Q\) lần lượt là trung điểm của \(SB,AB,CD,SC\). Chứng minh rằng:
a) \(AB \bot \left( {MNPQ} \right)\);
b) \(MQ \bot \left( {SAB} \right)\).
Phương pháp giải:
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Lời giải chi tiết:

a) Ta có: \(M\) là trung điểm của \(SB\)
\(Q\) là trung điểm của \(SC\)
\( \Rightarrow MQ\) là đường trung bình của \(\Delta SBC\)
\(\left. \begin{array}{l} \Rightarrow MQ\parallel BC\\BC \bot AB\end{array} \right\} \Rightarrow MQ \bot AB\)
\(M\) là trung điểm của \(SB\)
\(N\) là trung điểm của \(AB\)
\( \Rightarrow MN\) là đường trung bình của \(\Delta SAB\)
\(\left. \begin{array}{l} \Rightarrow MN\parallel SA\\SA \bot \left( {ABCD} \right)\end{array} \right\} \Rightarrow MN \bot \left( {ABCD} \right) \Rightarrow MN \bot AB\)
\(\left. \begin{array}{l}AB \bot MQ\\AB \bot MN\end{array} \right\} \Rightarrow AB \bot \left( {MNPQ} \right)\)
b) Ta có:
\(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right)\)
Lại có \(MQ\parallel BC\).
Vậy \(MQ \bot \left( {SAB} \right)\).
Vận dụng 2
Một kệ sách có bốn trụ chống và các ngăn làm bằng các tấm gỗ (Hình 18). Làm thể nào dùng một êke để kiểm tra xem các tấm gỗ có vuông góc với mỗi trụ chống và song song với nhau hay không? Giải thích cách làm.

Phương pháp giải:
Sử dụng các định lí:
‒ Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
‒ Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Lời giải chi tiết:
‒ Ta dùng êke kiểm tra hai mép tấm gỗ vuông góc với trụ chống thì tấm gỗ vuông góc với trụ chống.
‒ Ta kiểm tra tấm gỗ vuông góc với các trụ chống thì các trụ chống song song với nhau.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 60, 61, 62 SGK Toán 11 tập 2 - Chân trời sáng tạo timdapan.com"







