Đề thi kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Nam Từ Liêm
Giải chi tiết đề thi kì 1 môn toán lớp năm 2019 - 2020 phòng GDĐT Nam Từ Liêm với cách giải nhanh và chú ý quan trọng
I. TRẮC NGHIỆM (2 điểm) Chọn chữ cái trước câu trả lời đúng
Câu 1. Một hình thang có độ dài hai đáy là \(6cm\) và \(10cm\). Độ dài đường trung bình của hình thang đó là:
A. \(14cm\) B. \(7cm\)
C. \(8cm\) D. Một kết quả khác
Câu 2. Hai đường chéo cũng hình vuông có tính chất:
A. Bằng nhau, vuông góc với nhau.
B. Cắt nhau tại trung điểm của mỗi đường.
C. Là tia phân giác của các góc của hình vuông
D. Cả A, B, C
Câu 3. Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình nào sau đây?
A. Hình thang cân B. Hình bình hành
C. Hình chữ nhật D. Hình thoi
Câu 4. Một hình chữ nhật có kích thước là \(7dm\) và \(2dm\) thì có diện tích là:
A. \(14dm\) B. \(7d{m^2}\)
C. \(14d{m^3}\) D. \(14d{m^2}\)
Câu 5. \({\left( {x - y} \right)^2}\) bằng:
A. \({x^2} + {y^2}\) B. \({x^2} - 2xy + {y^2}\)
C. \({y^2} - {x^2}\) D. \({x^2} - {y^2}\)
Câu 6. Phân thức \(\dfrac{{{x^2} - 1}}{{x - 1}}\) rút gọn bằng:
A. \(x\) B. \(2\)
C. \(x + 1\) D. \(x - 1\)
Câu 7. Giá trị của biểu thức \(\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)\) tại \(x = - 2\)
A. \( - 16\) B. \(0\)
C. \( - 14\) D. \(2\)
Câu 8. Phân thức \(\dfrac{{x - 3}}{{x\left( {x - 2} \right)}}\) xác định với giá trị:
A. \(x \ne 2\) B. \(x \ne 0\)
C. \(x \ne 2;\,\,x \ne 0\) D. \(x \ne 3\)
II. TỰ LUẬN (8 điểm)
Bài 1 (1,0 điểm): Phân thức các đa thức sau thành nhân tử:
\(a)\,\,5x{y^2} - 10xyz + 5x{z^2}\) \(b)\,\,{x^2} - 4{y^2} + x + 2y\)
Bài 2 (1,0 điểm): Tìm \(x\) biết:
\(a)\,\,x\left( {x - 3} \right) - x + 3 = 0\) \(b)\,\,\left( {2x - 1} \right)\left( {x - 5} \right) - 2{x^2} + 10x - 25 = 0\)
Bài 3 (2,0 điểm): Cho biểu thức \(A = \dfrac{{x + 1}}{{x - 2}} + \dfrac{{x - 1}}{{x + 2}} + \dfrac{{{x^2} + 4x}}{{4 - {x^2}}}\,\,\,\,\left( {x \ne \pm 2} \right)\)
a) Rút gọn biểu thức \(A\).
b) Tính giá trị biểu thức \(A\) khi \(x = 4\).
c) Tìm giá trị nguyên của \(x\) để biểu thức \(A\) nhận giá trị nguyên dương.
Bài 4 (3,5 điểm): Cho hình bình hành \(ABCD\) có \(AB = 2BC;\,\,E,F\) theo thứ tự là trung điểm của \(AB\) và \(CD\).
a) Chứng minh tứ giác \(DEBF\) là hình bình hành.
b) Chứng minh tứ giác \(AEFD\) là hình thoi.
c) Gọi \(M\) là giao điểm của \(DE\) và \(AF\); \(N\) là giao điểm của \(EC\) và \(BF\). Tứ giác \(MENF\) là hình gì? Vì sao?
d) Hình bình hành \(ABCD\) có thêm điều kiện gì thì tứ giác \(MENF\)là hình vuông. Khi đó tính diện tích của tứ giác\(MENF\)biết \(BC = 3cm\).
Bài 5 (0,5 điểm): Cho \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2}\) và \(a,b,c\) là \(3\) số khác \(0\).
Chứng minh : \(\dfrac{1}{{{a^3}}} + \dfrac{1}{{{b^3}}} + \dfrac{1}{{{c^3}}} = \dfrac{3}{{abc}}\).
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHUYÊN MÔN TIMDAPAN.COM
PHẦN TRẮC NGHIỆM
|
1C |
2D |
3C |
4D |
|
5B |
6C |
7A |
8C |
Câu 1 (TH):
Phương pháp
Sử dụng : Độ dài đường trung bình của hình thang bằng nửa tổng hai đáy.
Cách giải:
Độ dài đường trung bình của hình thang bằng \(\dfrac{{6 + 10}}{2} = 8\left( {cm} \right)\)
Chọn C
Câu 2 (NB):
Phương pháp :
Sử dụng tính chất của hình vuông.
Cách giải:
Hai đường chéo của hình vuông bằng nhau, vuông góc với nhau, giao nhau tại trung điểm mỗi đường và là tia phân giác các góc của hình vuông nên A, B, C đều đúng.
Chọn D
Câu 3 (TH):
Phương pháp
Sử dụng dấu hiệu nhận biết hình bình hành, hình chữ nhật
Cách giải:
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Vậy tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là hình chữ nhật.
Chọn C
Câu 4(TH):
Phương pháp
Diện tích hình chữ nhật có các kích thước \(a,b\) là \(S = ab.\)
Cách giải:
Diện tích hình chữ nhật là : \(S = 7.2 = 14d{m^2}\)
Chọn D
Câu 5 (TH):
Phương pháp :
Sử dụng hằng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)
Cách giải:
Ta có : \({\left( {x - y} \right)^2} = {x^2} - 2xy + {y^2}\)
Chọn B
Câu 6 (TH):
Phương pháp
Phân tích tử thức thành nhân tử bằng cách sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) rồi rút gọn phân thức
Cách giải:
Ta có : \(\dfrac{{{x^2} - 1}}{{x - 1}} = \dfrac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}} = x + 1\)
Chọn C
Câu 7 (VD):
Phương pháp
Dùng hằng đẳng thức \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\) để thu gọn biểu thức
Thay \(x = - 2\) vào biểu thức đã thu gọn rồi tính toán
Cách giải:
Ta có : \(\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right) = {x^3} - {2^3} = {x^3} - 8\)
Thay \(x = - 2\) vào \({x^3} - 8\) ta được : \({\left( { - 2} \right)^3} - 8 = - 8 - 8 = - 16\)
Chọn A
Câu 8 (VD):
Phương pháp
Phân thức \(\dfrac{A}{B}\) xác định khi \(B \ne 0.\)
Cách giải:
Phân thức \(\dfrac{{x - 3}}{{x\left( {x - 2} \right)}}\) xác định khi \(x.\left( {x - 2} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 2\end{array} \right.\)
Vậy \(x \ne 2;x \ne 0.\)
Chọn C
PHẦN TỰ LUẬN
Bài 1 (VD):
Phương pháp :
a) Sử dụng phương pháp đặt nhân tử chung và hằng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\) để phân tích thành nhân tử
b) Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) và phương pháp đặt nhân tử chung.
Cách giải:
\(a)\,\,5x{y^2} - 10xyz + 5x{z^2}\)\( = 5x\left( {{y^2} - 2yz + {z^2}} \right) = 5x{\left( {y - z} \right)^2}\)
\(b)\,\,{x^2} - 4{y^2} + x + 2y\)\( = \left( {x - 2y} \right)\left( {x + 2y} \right) + \left( {x + 2y} \right) = \left( {x + 2y} \right)\left( {x - 2y + 1} \right)\)
Bài 2 (VD):
Phương pháp :
a) Sử dụng phương pháp đặt nhân tử chung để biến đổi về dạng \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)
b) Nhân đa thức với đa thức rồi rút gọn vế trái đưa về dạng tìm \(x\) đã biết.
Cách giải:
\(a)\,\,x\left( {x - 3} \right) - x + 3 = 0\)
\(\begin{array}{l} \Leftrightarrow x\left( {x - 3} \right) - \left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\end{array}\)
Vậy \(x = 1;x = 3.\)
\(b)\,\,\left( {2x - 1} \right)\left( {x - 5} \right) - 2{x^2} + 10x - 25 = 0\)
\(\begin{array}{l} \Leftrightarrow \,2{x^2} - 10x - x + 5 - 2{x^2} + 10x - 25 = 0\\ \Leftrightarrow - x - 20 = 0\\ \Leftrightarrow x = - 20\end{array}\)
Vậy \(x = - 20.\)
Bài 3 (VD):
Phương pháp :
a) Qui đồng mẫu thức rồi cộng trừ và rút gọn phân thức
b) Thay \(x = 4\left( {tmdk} \right)\) vào phân thức vừa thu gọn rồi tính toán
c) Biến đổi \(A\) về dạng \(A = m + \dfrac{b}{{B\left( x \right)}}\) với \(m,b \in Z.\)
Từ đó để \(A\) có giá trị nguyên thì \(B\left( x \right) \in U\left( b \right)\)
Sau đó lập luận để \(A\) mang giá trị nguyên dương.
Cách giải:
Cho biểu thức \(A = \dfrac{{x + 1}}{{x - 2}} + \dfrac{{x - 1}}{{x + 2}} + \dfrac{{{x^2} + 4x}}{{4 - {x^2}}}\,\,\,\,\left( {x \ne \pm 2} \right)\)
a) Rút gọn biểu thức \(A\).
Với \(x \ne \pm 2\) ta có :
\(\begin{array}{l}A = \dfrac{{x + 1}}{{x - 2}} + \dfrac{{x - 1}}{{x + 2}} + \dfrac{{{x^2} + 4x}}{{4 - {x^2}}}\,\\ = \dfrac{{x + 1}}{{x - 2}} + \dfrac{{x - 1}}{{x + 2}} - \dfrac{{{x^2} + 4x}}{{{x^2} - 4}}\end{array}\)
\( = \dfrac{{\left( {x + 1} \right)\left( {x + 2} \right) + \left( {x - 1} \right)\left( {x - 2} \right) - \left( {{x^2} + 4x} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \dfrac{{{x^2} + 3x + 2 + {x^2} - 3x + 2 - {x^2} - 4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\(\begin{array}{l} = \dfrac{{{x^2} - 4x + 4}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\\ = \dfrac{{{{\left( {x - 2} \right)}^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\\ = \dfrac{{x - 2}}{{x + 2}}\end{array}\)
Vậy \(A = \dfrac{{x - 2}}{{x + 2}}\) với \(x \ne \pm 2.\)
b) Tính giá trị biểu thức \(A\) khi \(x = 4\).
Thay \(x = 4\left( {tmdk} \right)\) vào biểu thức \(A = \dfrac{{x - 2}}{{x + 2}}\) ta được :
\(A = \dfrac{{4 - 2}}{{4 + 2}} = \dfrac{2}{6} = \dfrac{1}{3}\)
Vậy \(A = \dfrac{1}{3}\) khi \(x = 4.\)
c) Tìm giá trị nguyên của \(x\) để biểu thức \(A\) nhận giá trị nguyên dương.
Ta có \(A = \dfrac{{x - 2}}{{x + 2}}\) với \(x \ne \pm 2.\)
Xét \(A = \dfrac{{x - 2}}{{x + 2}} = \dfrac{{x + 2 - 4}}{{x + 2}} = 1 - \dfrac{4}{{x + 2}}\)
Để \(A\) có giá trị nguyên thì \(\dfrac{4}{{x + 2}}\) có giá trị nguyên
Suy ra \(\left( {x + 2} \right) \in U\left( 4 \right) = \left\{ { - 1;1; - 2;2; - 4;4} \right\}\)
Ta có bảng sau :
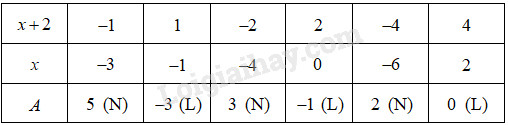
Vì \(A\) có giá trị nguyên dương nên ta có \(x \in \left\{ { - 3; - 4; - 6} \right\}\)
Bài 4 (VD):
Phương pháp :
a) Tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành
b) Hình bình hành có hai cạnh kề bằng nhau là hình thoi
c) Tứ giác có hai cặp cạnh đối song song là hình bình hành
Hình bình hành có 1 góc vuông là hình chữ nhật
d) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
Diện tích hình vuông cạnh \(a\) bằng \({a^2}.\)
Cách giải:
Cho hình bình hành \(ABCD\) có \(AB = 2BC;\,\,E,F\) theo thứ tự là trung điểm của \(AB\) và \(CD\).
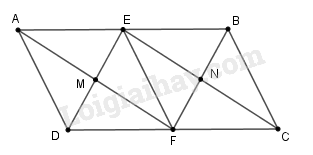
a) Chứng minh tứ giác \(DEBF\) là hình bình hành.
Xét hình bình hành \(ABCD\) có \(AB//CD \Rightarrow BE//DF;AE//DF\); \(AB = CD\) mà \(E,F\) lần lượt là trung điểm của \(AB,CD\) nên \(AE = EB = DF = FC = \dfrac{{AB}}{2}\).
Xét tứ giác \(DEBF\) có \(AB//DF;EB = DF\left( {cmt} \right)\) nên \(DEBF\) là hình bình hành (dhnb)
b) Chứng minh tứ giác \(AEFD\) là hình thoi.
Xét tứ giác \(ABCD\) có \(AB = 2BC \Rightarrow AB = 2AD \Rightarrow AD = \dfrac{{AB}}{2}\)
Do đó \(AE = AD = \dfrac{{AB}}{2}.\)
Xét tứ giác \(AEFD\) có \(AE//DF;AE = DF = \dfrac{{AB}}{2}\) (cmt) nên \(AEFD\) là hình bình hành (dhnb)
Lại có \(AE = AD = \dfrac{{AB}}{2}\,\left( {cmt} \right)\) nên hình bình hành \(AEFD\) là hình thoi (dhnb)
c) Gọi \(M\) là giao điểm của \(DE\) và \(AF\); \(N\) là giao điểm của \(EC\) và \(BF\). Tứ giác \(MENF\) là hình gì? Vì sao?
Xét tứ giác \(AECF\) có \(\left\{ \begin{array}{l}AE//FC\\AE = FC\left( { = \dfrac{{AB}}{2}} \right)\end{array} \right. \Rightarrow AECF\) là hình bình hành.
Suy ra \(AF//EC\) hay \(EN//MF\)
Vì \(EBFD\) là hình bình hành (theo câu a)) nên \(ED//BF \Rightarrow EM//FN\)
Xét tứ giác \(EMFN\) có \(EN//MF\) và \(EM//FN\) nên \(EMFN\) là hình bình hành (dhnb)
Vì \(AEFD\) là hình thoi (theo câu b) nên \(AF \bot DE\) (tính chất)
Suy ra \(\widehat {EMF} = {90^0} \Rightarrow \) hình bình hành \(EMFN\) có 1 góc vuông nên nó là hình chữ nhật (dhnb)
d) Hình bình hành \(ABCD\) có thêm điều kiện gì thì tứ giác \(MENF\)là hình vuông. Khi đó tính diện tích của tứ giác\(MENF\)biết \(BC = 3cm\).
Theo câu c) ta có \(MENF\) là hình chữ nhật.
Để hình chữ nhật \(MENF\) là hình vuông thì \(EM = EN\)
Vì \(AEFD\) là hình thoi nên \(M\) là trung điểm của \(ED.\)
Chứng minh tương tự ta cũng có \(EBCF\) là hình thoi nên \(N\) là trung điểm của \(EC.\)
Từ đó \(EM = EN \Leftrightarrow ED = EC\) suy ra tam giác \(EDC\) cân tại \(E\), lại có \(EF\) là đường trung tuyến của \(\Delta EDC\) nên \(EF\) cũng là đường cao \( \Rightarrow EF \bot DC.\)
Vì \(AEFD\) là hình thoi nên \(EF//AD\)
Suy ra \(AD \bot DC\)
Từ đó hình bình hành \(ABCD\) có \(AD \bot DC\) nên nó là hình chữ nhật.
Vậy để \(MENF\) là hình vuông thì \(ABCD\) là hình chữ nhật.
+) Ta có: \(BC = AD = EF = 3cm\) (tính chất)
Đặt \(ME = x\left( {x > 0} \right)\)
Xét hình vuông \(MENF\) có \(ME = MF = x\)
Áp dụng định lý Pytago cho tam giác vuông \(MEF\) ta có:
\(\begin{array}{l}M{E^2} + M{F^2} = E{F^2}\\ \Leftrightarrow {x^2} + {x^2} = {4^2}\\ \Leftrightarrow 2{x^2} = 16\\ \Leftrightarrow {x^2} = 8\end{array}\)
Diện tích hình vuông \(MENF\) là \(S = M{E^2} = {x^2} = 8\left( {c{m^2}} \right)\)
Bài 5 (VDC):
Phương pháp :
Áp dụng hằng đẳng thức \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2ac + 2bc\) và \({\left( {a + b} \right)^3} = {a^3} + {b^3} + 3ab\left( {a + b} \right)\)
Cách giải:
Ta có : \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2}\)\( + 2\left( {ab + ac + bc} \right)\)
Mà theo đề bài \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2}\)
Suy ra \(2\left( {ab + ac + bc} \right) = 0 \)\(\Leftrightarrow ab + ac + bc = 0\)
\(\begin{array}{l} \Leftrightarrow ab + ac = - bc\\ \Leftrightarrow {\left( {ab + ac} \right)^3} = - {b^3}{c^3}\\ \Leftrightarrow {a^3}{b^3} + {a^3}{c^3} + 3{a^2}bc\left( {ab + ac} \right) = - {b^3}{c^3}\\ \Leftrightarrow {a^3}{b^3} + {a^3}{c^3} + {b^3}{c^3} = - 3{a^2}bc.\left( { - bc} \right)\\ \Leftrightarrow {a^3}{b^3} + {a^3}{c^3} + {b^3}{c^3} = 3{a^2}{b^2}{c^2}\end{array}\)
Mà \(a,b,c \ne 0\) nên ta có
\(\begin{array}{l}{a^3}{b^3} + {a^3}{c^3} + {b^3}{c^3} = 3{a^2}{b^2}{c^2}\\ \Leftrightarrow \dfrac{{{a^3}{b^3} + {a^3}{c^3} + {b^3}{c^3}}}{{{a^3}{b^3}{c^3}}} = \dfrac{{3{a^2}{b^2}{c^2}}}{{{a^3}{b^3}{c^3}}}\\ \Leftrightarrow \dfrac{1}{{{a^3}}} + \dfrac{1}{{{b^3}}} + \dfrac{1}{{{c^3}}} = \dfrac{3}{{abc}}\left( {dpcm} \right)\end{array}\)
HẾT
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Nam Từ Liêm timdapan.com"







