Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Phú Nhuận
Giải chi tiết đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Phú Nhuận với cách giải nhanh và chú ý quan trọng
Bài 1. (2,5 điểm) Thực hiện các phép tính:
a) \({\left( {3x - 2} \right)^2} - \left( {3x + 4} \right)\left( {3x - 4} \right)\)
b) \(\left( {{x^4} - {x^2} + 2x - 1} \right):\left( {{x^2} + x - 1} \right)\)
c) \(\dfrac{3}{{x - 3}} + \dfrac{{ - 6x}}{{{x^2} - 9}} + \dfrac{x}{{x + 3}}\)
Bài 2. (1,5 điểm) Phân tích đa thức sau thành nhân tử:
a) \(xy + {y^2} - x - y\)
b) \({x^2} - 4x - {y^2} + 4\)
c) \({x^2} - 4x - 4{y^2} + 8y\)
Bài 3. (1 điểm) Tìm \(x\), biết
a) \({\left( {x + 4} \right)^2} - \left( {x + 3} \right)\left( {x - 2} \right) = - 13\)
b) \(4{x^2} - 3\left( {2x - 5} \right) - 25 = 0\)
Bài 4. (0,75 điểm) Hai điểm \(A\) và \(B\) ở hai bờ của một hồ nước (hình vẽ) có độ đài đoạn thẳng DE bằng 120m.
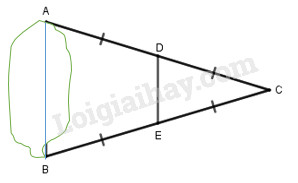
a) Hãy xác định khoảng cách AB.
b) Bạn An chèo một chiếc thuyền đi theo đường thẳng từ A đến B với vận tốc 2km/h. Hỏi thời gian bạn An đi từ A đến B? Biết rằng bạn An chèo liên tục và không nghỉ dọc đường.
Bài 5. (0,75 điểm) Nhà bạn Bình chuẩn bị lát gạch tầng trệt ngôi nhà (gồm phòng khách và phòng ăn). Phòng khách là hình chữ nhật có kích thước là 4m và 8m, phòng ăn cũng là hình chữ nhật có kích thước là 4m và 6m. Tiền gạch lát phòng khách là 280 000 đồng/m2; tiền gạch lát phòng ăn là 250 000 đồng/m2 và tiền công lát (tính cả vật liệu) là 80 000 đồng/m2. Hỏi nhà bạn Bình phải chuẩn bị ít nhất bao nhiêu tiền để lát gạch hết tầng trệt ngôi nhà?
Bài 6. (0,75 điểm) Tháng 11 vừa qua, có ngày Black Friday (thứ 6 đen – mua sắm siêu giảm giá). Một trung tâm thương mại tổ chức chương trình khuyến mãi giảm giá 60% cho các loại giày và 50% cho các loại quần áo. Bạn Việt mua một đôi giày có giá niêm yết là 4.000.000 đồng và một cái áo có giá niêm yết 2.500.000 đồng. Hỏi bạn Việt phải trả tất cả bao nhiêu tiền để mua cả hai món hàng trên?
Bài 7. (2,5 điểm) Cho \(\Delta ABC\) cân tại A có D là trung điểm cạnh BC. Gọi E là điểm đối xứng của A qua D.
a) Chứng minh tứ giác \(ABEC\) là hình thoi.
b) Từ C kẻ đường thẳng vuông góc với BC cắt tia BA tại F. Chứng minh tứ giác AECF là hình bình hành.
c) Gọi N là trung điểm của CF, kẻ CH vuông góc AB tại H. Chứng minh tam giác DHN vuông.
HẾT
HƯỚNG DẪN GIẢI CHI TIẾT
Thực hiện: Ban chuyên môn
Bài 1 (VD):
Phương pháp:
a) Sử dụng hằng đẳng thức khai triển và rút gọn biểu thức.
b) Phân tích đa thức bị chia thành nhân tử rồi thực hiện chia hai đa thức.
c) Quy đồng, rút gọn các phân thức.
Cách giải:
a) \({\left( {3x - 2} \right)^2} - \left( {3x + 4} \right)\left( {3x - 4} \right)\)
\(\begin{array}{l} = {\left( {3x} \right)^2} - 2.3x.2 + {2^2} - \left[ {{{\left( {3x} \right)}^2} - {4^2}} \right]\\ = 9{x^2} - 12x + 4 - 9{x^2} + 4\\ = - 12 + 8\end{array}\)
b) \(\left( {{x^4} - {x^2} + 2x - 1} \right):\left( {{x^2} + x - 1} \right)\)
\(\begin{array}{l} = \left[ {{x^4} - \left( {{x^2} - 2x + 1} \right)} \right]:\left( {{x^2} + x - 1} \right)\\ = \left[ {{{\left( {{x^2}} \right)}^2} - {{\left( {x - 1} \right)}^2}} \right]:\left( {{x^2} + x - 1} \right)\\ = \left[ {\left( {{x^2} - x + 1} \right)\left( {{x^2} + x - 1} \right)} \right]:\left( {{x^2} + x - 1} \right)\\ = {x^2} - x + 1\end{array}\)
c) \(\dfrac{3}{{x - 3}} + \dfrac{{ - 6x}}{{{x^2} - 9}} + \dfrac{x}{{x + 3}}\) (ĐK: \(x \ne \pm 3\))
\(\begin{array}{l} = \dfrac{3}{{x - 3}} + \dfrac{{ - 6x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} + \dfrac{x}{{x + 3}}\\ = \dfrac{{3\left( {x + 3} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} + \dfrac{{ - 6x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} + \dfrac{{x\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{3x + 9 - 6x + {x^2} - 3x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{{x^2} - 6x + 9}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{{{\left( {x - 3} \right)}^2}}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{x - 3}}{{x + 3}}\end{array}\)
Bài 2 (VD):
Phương pháp:
a) Tách nhóm các số hạng, đặt nhân tử chung.
b) Nhóm hạng tử kết hợp dùng hằng đẳng thức.
c) Nhóm hạng tử kết hợp dùng hằng đẳng thức và đặt nhân tử chung.
Cách giải:
a) \(xy + {y^2} - x - y\)
\(\begin{array}{l} = \left( {xy + {y^2}} \right) - \left( {x + y} \right)\\ = y\left( {x + y} \right) - \left( {x + y} \right)\\ = \left( {x + y} \right)\left( {y - 1} \right)\end{array}\)
b) \({x^2} - 4x - {y^2} + 4\)
\(\begin{array}{l} = \left( {{x^2} - 4x + 4} \right) - {y^2}\\ = {\left( {x - 2} \right)^2} - {y^2}\\ = \left( {x - 2 - y} \right)\left( {x - 2 + y} \right)\\ = \left( {x - y - 2} \right)\left( {x + y - 2} \right)\end{array}\)
c) \({x^2} - 4x - 4{y^2} + 8y\)
\(\begin{array}{l} = \left( {{x^2} - 4{y^2}} \right) - \left( {4x - 8y} \right)\\ = \left( {x - 2y} \right)\left( {x + 2y} \right) - 4\left( {x - 2y} \right)\\ = \left( {x - 2y} \right)\left( {x + 2y - 4} \right)\end{array}\)
Bài 3 (VD):
Phương pháp:
a) Khai triển hằng đẳng thức, rút gọn vế trái.
Sử dụng các quy tắc chuyển vế đổi dấu tìm \(x\).
b) Phân tích vế trái thành nhân tử, sử dụng \(AB = 0\) thì \(A = 0\) hoặc \(B = 0\).
Cách giải:
a) \({\left( {x + 4} \right)^2} - \left( {x + 3} \right)\left( {x - 2} \right) = - 13\)
\(\begin{array}{l}\left( {{x^2} + 8x + 16} \right) - \left( {{x^2} + 3x - 2x - 6} \right) = - 13\\{x^2} + 8x + 16 - {x^2} - 3x + 2x + 6 + 13 = 0\\7x + 35 = 0\\7x = - 35\\x = - 5\end{array}\)
Vậy \(x = - 5\).
b) \(4{x^2} - 3\left( {2x - 5} \right) - 25 = 0\)
\(\begin{array}{l}\left( {4{x^2} - 25} \right) - 3\left( {2x - 5} \right) = 0\\\left( {2x - 5} \right)\left( {2x + 5} \right) - 3\left( {2x - 5} \right) = 0\\\left( {2x - 5} \right)\left( {2x + 5 - 3} \right) = 0\\\left( {2x - 5} \right)\left( {2x + 2} \right) = 0\end{array}\)
TH1: \(2x - 5 = 0\)
\(\begin{array}{l}2x = 5\\x = \dfrac{5}{2}\end{array}\)
TH2: \(2x + 2 = 0\)
\(\begin{array}{l}2x = - 2\\x = - 1\end{array}\)
Vậy \(x = \dfrac{5}{2}\) hoặc \(x = - 1\).
Bài 4 (VD):
Phương pháp:
a) Sử dụng tính chất đường trung bình của tam giác: Đường trung bình song song và bằng nửa cạnh đáy.
b) Sử dụng công thức: Quãng đường bằng vận tốc \( \times \) thời gian.
Cách giải:
a) Hãy xác định khoảng cách AB.
Xét tam giác ABC có: D là trung điểm của AC, E là trung điểm của BC nên DE là đường trung bình của tam giác ABC
\( \Rightarrow DE = \dfrac{1}{2}AB\) \( \Rightarrow AB = 2DE = 2.120 = 240\left( m \right)\).
Vậy khoảng cách AB là \(240m\).
b) Bạn An chèo một chiếc thuyền đi theo đường thẳng từ A đến B với vận tốc 2km/h. Hỏi thời gian bạn An đi từ A đến B? Biết rằng bạn An chèo liên tục và không nghỉ dọc đường.
Đổi \(240m = 0,24km\).
Thời gian bạn An chèo thuyền từ A đến B là:
\(\dfrac{{0,24}}{2} = 0,12\) (giờ)\( = 7,2\) (phút)
Vậy An chèo thuyền từ A đến B hết \(7,2\) phút.
Bài 5 (VD):
Phương pháp :
Tính tiền gạch lát phòng khách
Tính tiền gạch lát phòng ăn
Tình tiền công lát gạch
Tính tổng số tiền
Cách giải:
Diện tích phòng khách là : \(4.8 = 32\left( {{m^2}} \right)\)
Diện tích phòng ăn là : \(4.6 = 24\left( {{m^2}} \right)\)
Tổng diện tích hai phòng là : \(32 + 24 = 56\left( {{m^2}} \right)\)
Số tiền gạch lát phòng khách là : \(32.280000 = 8960000\) đồng
Số tiền gạch lát phòng ăn là : \(24.250000 = 6000000\) đồng
Số tiền công lát cả hai phòng là : \(56.80000 = 4480000\) đồng
Tổng số tiền cần dùng là : \(8960000 + 6000000 + 4480000 = 19440000\) đồng.
Bài 6 (VD):
Phương pháp :
Tính số tiền giày sau khi giảm giá
Tính số tiền áo sau khi giảm giá
Tính tổng số tiền
Cách giải:
Tiền giày bạn Việt phải trả là : \(40\% .4000000 = 1600000\) đồng
Tiền áo bạn Việt phải trả là : \(50\% .25000000 = 1250000\) đồng
Tổng số tiền bạn Việt phải trả là :
\(1600000 + 1250000 = 1850000\) đồng.
Bài 7 (VD):
Phương pháp :
a) Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành
Hình bình hành có hai đường chéo vuông góc là hình thoi
b) Tứ giác có 2 cặp cạnh đối song song là hình bình hành
c) Sử dụng tính chất : Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền
Cách giải:
Cho \(\Delta ABC\) cân tại A có D là trung điểm cạnh BC. Gọi E là điểm đối xứng của A qua D.
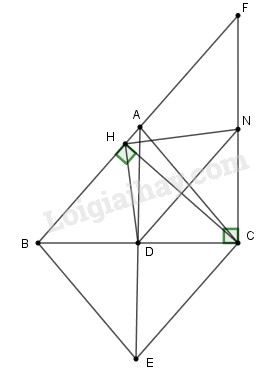
a) Chứng minh tứ giác \(ABEC\) là hình thoi.
Vì tam giác ABC cân tại A có AD là đường trung tuyến nên AD cũng là đường cao.
Suy ra \(AD \bot BC\) hay \(AE \bot BC\)
Xét tứ giác ABEC có D là trung điểm của BC (gt) và D là trung điểm của AE (do E đối xứng với A qua D) nên hai đường chéo AE và BC giao nhau tại trung điểm mỗi đường.
Do đó, tứ giác ABEC là hình bình hành
Lại có \(AE \bot BC\left( {cmt} \right)\) nên \(ABEC\) là hình thoi (dhnb)
b) Từ C kẻ đường thẳng vuông góc với BC cắt tia BA tại F. Chứng minh tứ giác AECF là hình bình hành
Do \(ABEC\) là hình bình hành ( câu a) nên \(AB//EC \Rightarrow AF//EC\) (1)
Lại có \(AD//CF\) (do cùng vuông góc với \(BC\)) nên \(AE//CF\) (2)
Từ (1) và (2) suy ra tứ giác \(AECF\) là hình bình hành (vì có 2 cặp cạnh đối song song)
c) Gọi N là trung điểm của CF, kẻ CH vuông góc AB tại H. Chứng minh tam giác DHN vuông.
Xét tam giác vuông \(BHC\) có \(HD\) là đường trung tuyến ứng với cạnh huyền nên \(HD = BD = \dfrac{{BC}}{2}\)
Suy ra \(\Delta HBD\) cân tại \(D \Rightarrow \widehat {HBD} = \widehat {BHD}\) (tính chất)
Xét tam giác vuông \(CHF\) có \(HN\) là đường trung tuyến ứng với cạnh huyền nên \(HN = NF = \dfrac{{FC}}{2}\)
Suy ra \(\Delta HNF\) cân tại \(N \Rightarrow \widehat {NHF} = \widehat {NFH}\) (tính chất)
Suy ra \(\widehat {BHD} + \widehat {HNF} = \widehat {HBD} + \widehat {HFN}\)
Xét tam giác \(BCF\) vuông tại \(C\) có \(\widehat {HBD} + \widehat {HFN} = {90^0}\)
Nên \(\widehat {BHD} + \widehat {HNF} = \widehat {HBD} + \widehat {HFN}\)\( = {90^0}\)
Mà \(\widehat {BHD} + \widehat {HNF} + \widehat {DHN} = {180^0}\) nên \(\widehat {DHN} = {90^0}\)
Do đó tam giác \(DHN\) vuông tại \(H.\)
Hết
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Phú Nhuận timdapan.com"







