Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GD&ĐT Quận 12
Giải chi tiết đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GD&ĐT Quận 12 với cách giải nhanh và chú ý quan trọng
Bài 1. (2 điểm) Thực hiện phép tính:
a) \({\left( {2x + 3} \right)^2} - 4x\left( {x + 3} \right)\)
b) \(\left( {2{x^2}{y^4} - 15x{y^2}} \right):5x{y^2} - \dfrac{2}{5}x{y^2}\)
c) \(\dfrac{x}{{x - 2}} + \dfrac{{2 - x}}{{x + 2}} + \dfrac{{6 - 5x}}{{{x^2} - 4}}\)
Bài 2. (2 điểm) Phân tích đa thức sau thành nhân tử:
a) \(3{x^3}y - 6{x^2}{y^2} + 3x{y^3}\)
b) \({x^2} - 3x - 40\)
Bài 3. (1,5 điểm) Tìm \(x\)
a) \({\left( {2x - 1} \right)^2} - 25 = 0\)
b) \({x^2} + 5x + 6 = 0\)
Bài 4. (0,5 điểm) Ngày thứ nhất, giá xăng RON 95 là \(17\,476\) đồng/lít. Ngày thứ hai, giá xăng tăng \(1\% \)/lít. Ngày thứ ba, giá xăng tiếp tục tăng \(2\% \)/lít so với ngày thứ hai. Hỏi ngày thứ ba, giá xăng RON 95 là bao nhiêu tiền một lít?
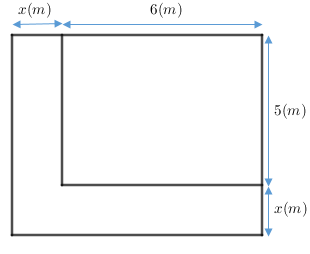
Bài 5. (1 điểm) Người ta làm một lối đi theo chiều dài và chiều rộng của một hồ nước hình chữ nhật (như hình vẽ). Em hãy tính chiều rộng \(x\) (mét, điều kiện \(x > 0\)) của lối đi, biết rằng lối đi có diện tích bằng \(26\left( {{m^2}} \right)\).
Bài 6. (3 điểm)
Cho \(\Delta ABC\) vuông tại \(A\) \(\left( {AB < AC} \right)\) và đường cao \(AH\). Từ \(H\) kẻ \(HE \bot AB\), \(HF \bot AC\) \(\left( {E \in AB,F \in AC} \right)\).
a) Chứng minh tứ giác \(AEHF\) là hình chữ nhật.
b) Gọi \(D\) là điểm đối xứng của \(A\) qua \(F\). Chứng minh \(DHEF\) là hình bình hành.
c) Gọi \(I\) là giao điểm của \(EF\) và \(AH\); \(M\) là trung điểm của \(BC\). Qua \(A\) kẻ tia \(Ax\) vuông góc với đường thẳng \(MI\) cắt tia \(CB\) tại \(K\). Chứng minh 4 điểm \(K,E,I,F\) thẳng hàng.
HẾT
HƯỚNG DẪN GIẢI CHI TIẾT
Thực hiện: Ban chuyên môn
Bài 1 (VD):
Phương pháp:
a) Sử dụng hằng đẳng thức khai triển và rút gọn biểu thức.
b) Thực hiện chia đa thức cho đơn thức: Chia từng đơn thức trong đa thức cho đơn thức đã cho rồi cộng các hệ số với nhau.
c) Quy đồng, rút gọn các phân thức.
Cách giải:
a) \({\left( {2x + 3} \right)^2} - 4x\left( {x + 3} \right)\)
\(\begin{array}{l} = {\left( {2x} \right)^2} + 2.2x.3 + {3^2} - \left( {4{x^2} + 12x} \right)\\ = 4{x^2} + 12x + 9 - 4{x^2} - 12x\\ = \left( {4{x^2} - 4{x^2}} \right) + \left( {12x - 12x} \right) + 9\\ = 9\end{array}\)
b) \(\left( {2{x^2}{y^4} - 15x{y^2}} \right):5x{y^2} - \dfrac{2}{5}x{y^2}\)
\(\begin{array}{l} = 2{x^2}{y^4}:5x{y^2} - 15x{y^2}:5x{y^2} - \dfrac{2}{5}x{y^2}\\ = \dfrac{2}{5}x{y^2} - 3 - \dfrac{2}{5}x{y^2}\\ = \left( {\dfrac{2}{5}x{y^2} - \dfrac{2}{5}x{y^2}} \right) - 3\\ = - 3\end{array}\)
c) \(\dfrac{x}{{x - 2}} + \dfrac{{2 - x}}{{x + 2}} + \dfrac{{6 - 5x}}{{{x^2} - 4}}\) (ĐK: \(x \ne \pm 2\))
\( = \dfrac{x}{{x - 2}} + \dfrac{{2 - x}}{{x + 2}} + \dfrac{{6 - 5x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \dfrac{{x\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\) \( + \dfrac{{\left( {2 - x} \right)\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)\( + \dfrac{{6 - 5x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \dfrac{{{x^2} + 2x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\) \( + \dfrac{{ - {x^2} + 4x - 4}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)\( + \dfrac{{6 - 5x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \dfrac{{{x^2} + 2x - {x^2} + 4x - 4 + 6 - 5x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \dfrac{{x + 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \dfrac{1}{{x - 2}}\).
Bài 2 (VD):
Phương pháp:
a) Đặt nhân tử chung kết hợp dùng hằng đẳng thức.
b) Tách nhóm các số hạng, đặt nhân tử chung.
Cách giải:
a) \(3{x^3}y - 6{x^2}{y^2} + 3x{y^3}\)
\(\begin{array}{l} = 3xy\left( {{x^2} - 2xy + {y^2}} \right)\\ = 3xy{\left( {x - y} \right)^2}\end{array}\)
b) \({x^2} - 3x - 40\)
\(\begin{array}{l} = {x^2} - 8x + 5x - 40\\ = x\left( {x - 8} \right) + 5\left( {x - 8} \right)\\ = \left( {x - 8} \right)\left( {x + 5} \right)\end{array}\)
Bài 3 (VD):
Phương pháp:
a) Sử dụng hằng đẳng thức đưa vế trái về dạng tích.
Chú ý: \(AB = 0\) thì \(A = 0\) hoặc \(B = 0\).
b) Phân tích vế trái thành nhân tử, sử dụng \(AB = 0\) thì \(A = 0\) hoặc \(B = 0\).
Cách giải:
a) \({\left( {2x - 1} \right)^2} - 25 = 0\)
\(\begin{array}{l}{\left( {2x - 1} \right)^2} - {5^2} = 0\\\left( {2x - 1 - 5} \right)\left( {2x - 1 + 5} \right) = 0\\\left( {2x - 6} \right)\left( {2x + 4} \right) = 0\end{array}\)
TH1: \(2x - 6 = 0\)
\(\begin{array}{l}2x = 6\\x = 3\end{array}\)
TH2: \(2x + 4 = 0\)
\(\begin{array}{l}2x = - 4\\x = - 2\end{array}\)
Vậy \(x = 3\) hoặc \(x = - 2\).
b) \({x^2} + 5x + 6 = 0\)
\(\begin{array}{l}{x^2} + 2x + 3x + 6 = 0\\x\left( {x + 2} \right) + 3\left( {x + 2} \right) = 0\\\left( {x + 2} \right)\left( {x + 3} \right) = 0\end{array}\)
\(x + 2 = 0\) hoặc \(x + 3 = 0\)
\(x = - 2\) hoặc \(x = - 3\).
Vậy \(x = - 2\) hoặc \(x = - 3\).
Bài 4 (VD):
Phương pháp:
Lần lượt tính giá xăng của ngày thứ hai và ngày thứ ba và kết luận.
Cách giải:
Giá xăng ngày thứ hai là:
\(17\,476 + 17\,476.1\% = 17\,650,76\) (đồng/lít)
Giá xăng ngày thứ ba là:
\(17\,650,76 + 17\,650,76.2\% = 18\,003,7752\) (đồng/lít)
Vậy ngày thứ ba, giá xăng là \(18\,003,7752\) đồng/lít.
Bài 5 (VD):
Phương pháp:
- Chia phần lối đi thành hai hình chữ nhật.
- Tính diện tích mỗi phần theo \(x\).
- Sử dụng dữ kiện diện tích để tìm \(x\).
Cách giải:
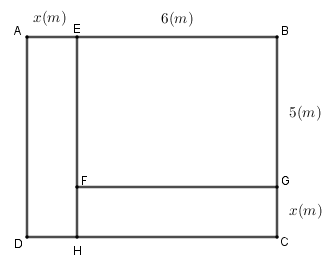
Diện tích hình chữ nhật \(AEHD\) là: \(x\left( {5 + x} \right)\).
Diện tích hình chữ nhật \(CHFG\) là: \(6x\).
Vì lối đi có diện tích là \(26{m^2}\) nên \(x\left( {5 + x} \right) + 6x = 26\)
\(\begin{array}{l}5x + {x^2} + 6x - 26 = 0\\{x^2} + 11x - 26 = 0\\{x^2} - 2x + 13x - 26 = 0\\x\left( {x - 2} \right) + 13\left( {x - 2} \right) = 0\\\left( {x - 2} \right)\left( {x + 13} \right) = 0\end{array}\)
Vì \(x > 0\) nên \(x - 2 = 0\) hay \(x = 2\).
Vậy chiều rộng lối đi là \(2m\).
Bài 6(VD):
Phương pháp:
a) Sử dụng dấu hiệu nhận biết hình chữ nhật: Tứ giác có ba góc vuông là hình chữ nhật
b) Sử dụng dấu hiệu nhận biết hình bình hành: Tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau là hình bình hành.
c) Chứng minh \(KI \bot AM\) bằng cách sử dụng tính chất ba đường cao của tam giác \(AMK\).
Chứng minh \(EI \bot AM\), từ đó suy ra ba điểm thẳng hàng.
Cách giải:
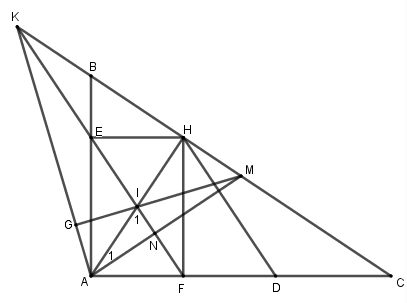
a) Chứng minh tứ giác \(AEHF\) là hình chữ nhật.
Ta có: \(\left\{ \begin{array}{l}HE \bot AB \Rightarrow \widehat {HEA} = {90^0}\\HF \bot AC \Rightarrow \widehat {HFA} = {90^0}\end{array} \right.\)
Xét tứ giác \(AEHF\) có: \(\widehat {HEA} = \widehat A = \widehat {HFA} = {90^0}\) nên là hình chữ nhật (Tứ giác có ba góc vuông là hình chữ nhật) (đpcm)
b) Gọi \(D\) là điểm đối xứng của \(A\) qua \(F\). Chứng minh \(DHEF\) là hình bình hành.
Do \(AEHF\) là hình chữ nhật (cmt) nên \(HE = AF\) (t/c) (1)
Mà \(D\) đối xứng với \(A\) qua \(F\) nên \(AF = FD\) (2)
Từ (1) và (2) suy ra \(HE = FD\) \(\left( { = AF} \right)\) (3)
Mà \(\left\{ \begin{array}{l}HE \bot AB\\AC \bot AB\end{array} \right.\) \( \Rightarrow HE//AC\) (từ vuông góc đến song song)
\( \Rightarrow HE//FD\) (4)
Từ (3) và (4) suy ra \(HEFD\) là hình bình hành (tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau).
c) Gọi \(I\) là giao điểm của \(EF\) và \(AH\); \(M\) là trung điểm của \(BC\). Qua \(A\) kẻ tia \(Ax\) vuông góc với đường thẳng \(MI\) cắt tia \(CB\) tại \(K\). Chứng minh 4 điểm \(K,E,I,F\) thẳng hàng.
Gọi \(G\) là giao điểm của \(MI\) và \(AK\) \( \Rightarrow MG \bot AK\).
Xét tam giác \(AMK\) có \(MG \bot AK,AH \bot MK\) nên \(MG,AH\) là các đường cao trong tam giác.
Mà \(I = MG \cap AH\) nên \(I\) là trực tâm của tam giác \( \Rightarrow KI \bot AM\) (5)
Gọi \(N\) là giao điểm của \(EF\) và \(AM\).
Tam giác \(ABC\) vuông tại \(A\), \(M\) là trung điểm của \(BC\) nên \(MA = MC = MB = \dfrac{1}{2}BC\) (t/c)
\( \Rightarrow \Delta AMC\) cân tại \(M\)\( \Rightarrow \widehat {MAC} = \widehat {MCA}\).
\(\widehat {HMA}\) là góc ngoài tam giác \(AMC\) nên \(\widehat {HMA} = \widehat {MAC} + \widehat {MCA} = 2\widehat {MCA}\) (6)
Xét \(\Delta IEA\) có \(IE = IA \Rightarrow \Delta IEA\) cân tại \(I\) \( \Rightarrow \widehat {IEA} = \widehat {IAE}\)
\(\widehat {{I_1}}\) là góc ngoài tam giác \(IEA\) nên \(\widehat {{I_1}} = \widehat {IEA} + \widehat {IAE} = 2\widehat {IAE}\) (7)
Mà \(\widehat {IAE} = \widehat {MCA}\) (cùng phụ \(\widehat {ABC}\)) (8)
Từ (6), (7), (8) suy ra \(\widehat {HMA} = \widehat {{I_1}}\) (9)
Tam giác \(AHM\) vuông tại \(H\) nên \(\widehat {{A_1}} + \widehat {HMA} = {90^0}\) (10)
Từ (9) và (10) suy ra \(\widehat {{A_1}} + \widehat {{I_1}} = {90^0}\).
Tam giác \(INA\) có \(\widehat {{A_1}} + \widehat {{I_1}} = {90^0}\) \( \Rightarrow \widehat {INA} = {180^0} - {90^0} = {90^0}\)
\( \Rightarrow EI \bot AM\) (11)
Từ (5) và (11) suy ra \(K,E,I\) thẳng hàng (tiên đề Ơ clit) hay bốn điểm \(K,E,I,F\) thẳng hàng (đpcm)
HẾT
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GD&ĐT Quận 12 timdapan.com"







