Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Quận 11
Giải chi tiết đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Quận 11 với cách giải nhanh và chú ý quan trọng
Bài 1. (3 điểm) Tính và rút gọn:
a) \(\left( {3x - 4} \right)\left( {x + 5} \right)\)
b) \(4x\left( {x - 3} \right) + {\left( {x - 5} \right)^2}\)
c) \(\dfrac{6}{{{x^2} + 4x}} + \dfrac{3}{{2x + 8}}\) \(\left( {x \ne 0,x \ne - 4} \right)\)
Bài 2. (1 điểm) Phân tích đa thức thành nhân tử:
a) \(2{x^3} - 8x\)
b) \(16{x^2} - 8x + 1 - 16{y^2}\)
Bài 3. (1 điểm) Tìm \(x\)
a) \(\left( {x - 2} \right)\left( {2x + 3} \right) = 0\)
b) \(2\left( {x + 5} \right) - {x^2} - 5x = 0\)
Bài 4. (0,75 điểm) Một mảnh đất hình chữ nhật có chiều dài bằng \({\left( {2x + 1} \right)^2}\) mét, chiều rộng bằng \(\left( {4{x^2} + x} \right)\) mét. Biết chiều dài hơn chiều rộng là 16 mét. Tính chiều rộng của mảnh đất trên.
Bài 5. (0,75 điểm) Chào mừng ngày Nhà giáo Việt Nam 20/11, trường của An tổ chức cho các học sinh khối 8 thi đấu bóng đá theo thể thức vòng tròn một lượt (mỗi đội đều gặp nhau một trận). Tổng số các trận thi đấu được tính bởi biểu thức \(T = \dfrac{{x\left( {x - 1} \right)}}{2}\) (\(T\) là tổng số trận đấu, \(x\) là số đội tham gia). Em hãy tính xem có bao nhiêu đội đã tham gia thi đấu, biết tổng số trận đấu là \(28\) trận.
Bài 6. (1 điểm) Hình bên là một phần của cái thang bằng gỗ, các bậc thang song song và cách đều nhau (AB//CD//EF, AC=CE=BD=DF). Cái thang vị gãy mất thanh CD nên cần được thay thế. Biết thanh AB dài 8cm và thanh EF dài 16cm. Hỏi cần mua thanh thay thế có chiều dài bao nhiêu?
Bài 7. (2,5 điểm) Cho \(\Delta ABC\) vuông tại A \(\left( {AB < AC} \right)\). Gọi D, E lần lượt là trung điểm các cạnh BC, AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm đoạn thẳng EF.
a) Chứng minh tứ giác BFCE là hình bình hành.
b) Chứng minh tứ giác BFEA là hình chữ nhật.
c) Vẽ AH là đường cao của tam giác ABC. Gọi M là trung điểm đoạn thẳng HC. Chứng minh \(FM \bot AM\).
HẾT
HƯỚNG DẪN GIẢI CHI TIẾT
Thực hiện: Ban chuyên môn
Bài 1 (VD):
Phương pháp:
a, Nhân các đa thức một biến với nhau và rút gọn.
b) Sử dụng hằng đẳng thức khai triển và rút gọn biểu thức.
c) Quy đồng, rút gọn các phân thức.
Cách giải:
a) \(\left( {3x - 4} \right)\left( {x + 5} \right)\)
\(\begin{array}{l} = 3{x^2} - 4x + 15x - 20\\ = 3{x^2} + 11x - 20\end{array}\)
b) \(4x\left( {x - 3} \right) + {\left( {x - 5} \right)^2}\)
\(\begin{array}{l} = 4{x^2} - 12x + {x^2} - 10x + 25\\ = \left( {4{x^2} + {x^2}} \right) - \left( {12x + 10x} \right) + 25\\ = 5{x^2} - 22x + 25\end{array}\)
c) \(\dfrac{6}{{{x^2} + 4x}} + \dfrac{3}{{2x + 8}}\) \(\left( {x \ne 0,x \ne - 4} \right)\)
\(\begin{array}{l} = \dfrac{6}{{x\left( {x + 4} \right)}} + \dfrac{3}{{2\left( {x + 4} \right)}}\\ = \dfrac{{6.2}}{{2x\left( {x + 4} \right)}} + \dfrac{{3x}}{{2x\left( {x + 4} \right)}}\\ = \dfrac{{12 + 3x}}{{2x\left( {x + 4} \right)}} = \dfrac{{3\left( {x + 4} \right)}}{{2x\left( {x + 4} \right)}}\\ = \dfrac{3}{{2x}}\end{array}\)
Bài 2 (VD):
Phương pháp:
Nhóm các hạng tử kết hợp dùng hằng đẳng thức và đặt nhân tử chung.
Cách giải:
a) \(2{x^3} - 8x\)
\(\begin{array}{l} = 2x\left( {{x^2} - 4} \right)\\ = 2x\left( {x - 2} \right)\left( {x + 2} \right)\end{array}\)
b) \(16{x^2} - 8x + 1 - 16{y^2}\)
\(\begin{array}{l} = \left[ {{{\left( {4x} \right)}^2} - 2.4x.1 + {1^2}} \right] - {\left( {4y} \right)^2}\\ = {\left( {4x - 1} \right)^2} - {\left( {4y} \right)^2}\\ = \left( {4x - 1 - 4y} \right)\left( {4x - 1 + 4y} \right)\\ = \left( {4x - 4y - 1} \right)\left( {4x + 4y - 1} \right)\end{array}\)
Bài 3 (VD):
Phương pháp:
a) Sử dụng \(AB = 0\) thì \(A = 0\) hoặc \(B = 0\).
b) Phân tích vế trái thành nhân tử, sử dụng \(AB = 0\) thì \(A = 0\) hoặc \(B = 0\).
Cách giải:
a) \(\left( {x - 2} \right)\left( {2x + 3} \right) = 0\)
\(\begin{array}{l}TH1:x - 2 = 0\\x = 0 + 2\\x = 2\\TH2:2x + 3 = 0\\2x = - 3\\x = - \dfrac{3}{2}\end{array}\)
Vậy \(x = 2\) hoặc \(x = - \dfrac{3}{2}\).
b) \(2\left( {x + 5} \right) - {x^2} - 5x = 0\)
\(\begin{array}{l}2\left( {x + 5} \right) - \left( {{x^2} + 5x} \right) = 0\\2\left( {x + 5} \right) - x\left( {x + 5} \right) = 0\\\left( {x + 5} \right)\left( {2 - x} \right) = 0\\TH1:x + 5 = 0\\x = 0 - 5\\x = - 5\\TH2:2 - x = 0\\x = 2 - 0\\x = 2\end{array}\)
Vậy \(x = - 5\) hoặc \(x = 2\).
Bài 4 (VD):
Phương pháp:
- Thiết lập biểu thức thể hiện chiều dài hơn chiều rộng 16 mét.
- Tìm \(x\) và kết luận.
Cách giải:
Vì chiều dài hơn chiều rộng \(16\) mét nên ta có:
\(\begin{array}{l}{\left( {2x + 1} \right)^2} - \left( {4{x^2} + x} \right) = 16\\4{x^2} + 4x + 1 - 4{x^2} - x = 16\\\left( {4{x^2} - 4{x^2}} \right) + \left( {4x - x} \right) = 16 - 1\\3x = 15\\x = 5\end{array}\)
Chiều rộng của hình chữ nhật là: \({4.5^2} + 5 = 105\left( m \right)\).
Vậy chiều rộng hình chữ nhật là \(105m\).
Bài 5 (VD):
Phương pháp:
Cho \(T = 28\) rồi tìm \(x.\)
Cách giải:
Gọi số đội tham gia là \(x\left( {x \in {N^*}} \right)\)
Vì tổng số trận đấu là 28 trận nên ta có:
\(\begin{array}{l}\dfrac{{x\left( {x - 1} \right)}}{2} = 28\\ \Leftrightarrow {x^2} - x = 56\\ \Leftrightarrow {x^2} - 8x + 7x - 56 = 0\\ \Leftrightarrow x\left( {x - 8} \right) + 7\left( {x - 8} \right) = 0\\ \Leftrightarrow \left( {x + 7} \right)\left( {x - 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 7 = 0\\x - 8 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 7\left( L \right)\\x = 8\left( N \right)\end{array} \right.\end{array}\)
Vậy có 8 đội tham gia thi đấu
Bài 6 (VD):
Phương pháp:
Sử dụng tính chất đường trung bình của hình thang
Cách giải:
Xét tứ giác ABFE có AB//EF nên ABFE là hình thang
Lại có CD//AB//EF và C là trung điểm AE, D là trung điểm BF nên CD là đường trung bình của hình thang ABFE.
Từ đó ta có: \(CD = \dfrac{{AB + EF}}{2}\) \( = \dfrac{{8 + 16}}{2} = 12cm\)
Vậy cần mua thanh thay thế dài 12cm.
Bài 7 (VD):
Phương pháp:
a) Sử dụng dấu hiệu nhận biết hình bình hành
b) Sử dụng dấu hiệu nhận biết hình bình hành
Dấu hiệu nhận biết hình chữ nhật
c) Sử dụng tính chất trực tâm và tính chất hình bình hành
Cách giải:
Cho \(\Delta ABC\) vuông tại A \(\left( {AB < AC} \right)\). Gọi D, E lần lượt là trung điểm các cạnh BC, AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm đoạn thẳng EF.
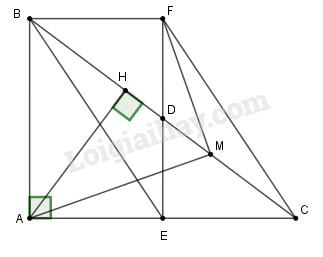
a) Chứng minh tứ giác BFCE là hình bình hành.
Xét tứ giác BFCE có D là trung điểm BC và D là trung điểm EF nên hai đường chéo BD và EF giao nhau tại trung điểm mỗi đường. Suy ra BFCE là hình bình hành (dhnb)
b) Chứng minh tứ giác BFEA là hình chữ nhật.
Vì BFCE là hình bình hành (câu a) nên BF//CE và \(BF = EC\) hay BF//AE và \(BF = AE\) (vì \(AE = EC\))
Nên tứ giác AEFB là hình bình hành (dhnb)
Lại có \(\widehat {BAE} = {90^0}\) nên hình bình hành \(AEFB\) là hình chữ nhật (dhnb)
c) Vẽ AH là đường cao của tam giác ABC. Gọi M là trung điểm đoạn thẳng HC. Chứng minh \(FM \bot AM\).
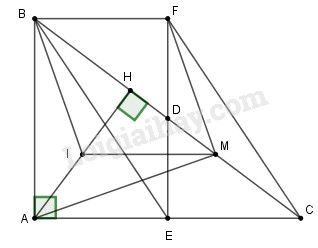
Gọi I là trung điểm của AH. Xét tam giác HAC có MI là đường trung bình nên \(MI//AC,MI = \dfrac{1}{2}AC\) (1)
Lại có \(AC \bot AB \Rightarrow MI \bot AB\)
Xét tam giác \(ABM\) có \(AH \bot BM,MI \bot AB\) mà \(I \in AH\) nên \(I\) là trực tâm tam giác \(ABM\)
Suy ra \(BI \bot AM\)
Vì BFCE là hình bình hành (câu a) nên \(BF = EC = \dfrac{{AC}}{2};BF//AC\) (2)
Từ (1) và (2) suy ra \(IM//BF//AC,\) \(IM = BF = \dfrac{{AC}}{2}\)
Do đó, tứ giác BIMF là hình bình hành (dhnb)
Suy ra \(BI//FM\) mà \(BI \bot AM \Rightarrow FM \bot AM\) (đpcm)
Hết
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi học kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Quận 11 timdapan.com"







