Giải câu 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 trang 64, 65, 66
Giải Cùng em học Toán lớp 4 tập 2 câu 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 trang 64, 65, 66 với lời giải chi tiết. Câu 3 : Trong số 5 371 907 : a) Chữ số 5 thuộc hàng …… lớp …… ; b) Chữ số 9 thuộc hàng …… lớp ……
Bài 1
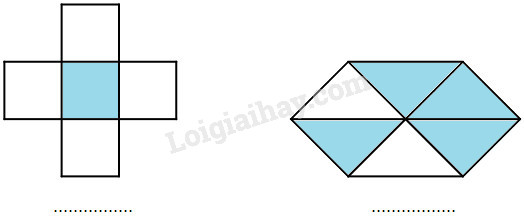
Viết phân số chỉ phần đã tô màu của mỗi hình dưới đây vào chỗ chấm:
Phương pháp giải:
Quan sát hình vẽ, tìm số ô được tô màu và tổng số ô. Phân số chỉ phần đã tô màu có tử số là số ô được tô màu và mẫu số là tổng số ô.
Lời giải chi tiết:
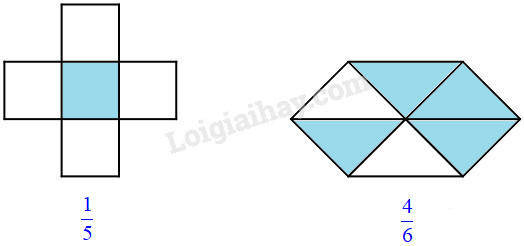
Bài 2
Viết tỉ số thích hợp vào ô trống (theo mẫu):
|
\(a\) |
\(b\) |
Tỉ số của \(a\) và \(b\) |
Tỉ số của \(b\) và \(a\) |
|
\(3l\) |
\(4l\) |
\(\dfrac{3}{4}\) |
\(\dfrac{4}{3}\) |
|
\(3kg\) |
\(7kg\) |
|
|
|
\(9\) |
\(10\) |
|
|
Phương pháp giải:
Tỉ số của \(a\) và \(b\) là \(a:b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).
Tương tự, tỉ số của \(b\) và \(a\) là \(b:a\) hay \(\dfrac{b}{a}\) (\(a\) khác \(0\)).
Lời giải chi tiết:
|
\(a\) |
\(b\) |
Tỉ số của \(a\) và \(b\) |
Tỉ số của \(b\) và \(a\) |
|
\(3l\) |
\(4l\) |
\(\dfrac{3}{4}\) |
\(\dfrac{4}{3}\) |
|
\(3kg\) |
\(7kg\) |
\(\dfrac{3}{7}\) |
\(\dfrac{7}{3}\) |
|
\(9\) |
\(10\) |
\(\dfrac{9}{10}\) |
\(\dfrac{10}{9}\) |
Bài 3
Viết tiếp vào chỗ chấm cho thích hợp:
Trong số 5 381 907:
a) Chữ số 5 thuộc hàng …… lớp ……
b) Chữ số 9 thuộc hàng …… lớp ……
Phương pháp giải:
- Các chữ số từ phải sang trái lần lượt thuộc hàng đơn vị, hàng chục, hàng trăm, hàng nghìn, hàng chục nghìn, hàng trăm nghìn ...
- Áp dụng lý thuyết về lớp:
+ Lớp đơn vị gồm hàng đơn vị, hàng chục, hàng trăm.
+ Lớp nghìn gồm hàng nghìn, hàng chục nghìn, hàng trăm nghìn.
+ Lớp triệu gồm hàng triệu, hàng chục triệu, hàng chục triệu.
Lời giải chi tiết:
Trong số 5 381 907:
a) Chữ số 5 thuộc hàng triệu, lớp triệu.
b) Chữ số 9 thuộc hàng trăm, lớp đơn vị.
Bài 4
Viết tiếp vào chỗ chấm cho thích hợp :
a) 5km2 = …… m2
b) 23m2 73dm2 = …… dm2
Phương pháp giải:
Áp dụng cách đổi đơn vị đo diện tích: \(1k{m^2} = 1\,\,000\,\,000{m^2}\,;\,1{m^2} = 100d{m^2}\).
Lời giải chi tiết:
a) 5km2 = 5 000 000m2
b) 23m2 73dm2 = 2373dm2
Bài 5
Viết phân số thích hợp vào chỗ chấm:
Trong các phân số \(\dfrac{3}{4};\dfrac{9}{8};\dfrac{{19}}{{24}};\dfrac{{11}}{{11}};\dfrac{{17}}{{13}};\dfrac{{29}}{{29}}\), các phân số bé hơn 1 là:.........
Phương pháp giải:
Phân số có tử số bé hơn mẫu số thì phân số đó bé hơn \(1\).
Lời giải chi tiết:
Trong các phân số đã cho, các phân số bé hơn \(1\) là: \(\dfrac{3}{4}\,\,;\,\,\,\dfrac{{19}}{{24}}\).
Bài 6
Rút gọn các phân số:
\(\dfrac{{12}}{{36}} = \ldots \) \(\dfrac{{78}}{{45}} = \ldots \)
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
\(\dfrac{{12}}{{36}} = \dfrac{{12:12}}{{36:12}} = \dfrac{1}{3}\) \(\dfrac{{78}}{{45}} = \dfrac{{78:3}}{{45:3}} = \dfrac{{26}}{{15}}\)
Bài 7
Tính:
\(\dfrac{3}{5} + \dfrac{7}{{15}} = \ldots \)
\(\dfrac{{13}}{{17}} + \dfrac{{31}}{{34}} = \ldots \)
Phương pháp giải:
Muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi cộng hai phân số sau khi quy đồng.
Lời giải chi tiết:
\(\dfrac{3}{5} + \dfrac{7}{{15}} = \dfrac{9}{{15}} + \dfrac{7}{{15}} = \dfrac{{16}}{{15}}\) \(\dfrac{{13}}{{17}} + \dfrac{{31}}{{34}} = \dfrac{{26}}{{34}} + \dfrac{{31}}{{34}} = \dfrac{{57}}{{34}}\)
Bài 8
Khoanh vào chữ đặt trước câu trả lời đúng:
Cho biết hình chữ nhật và hình bình hành dưới đây có cùng diện tích. Chu vi của hình chữ nhật là:
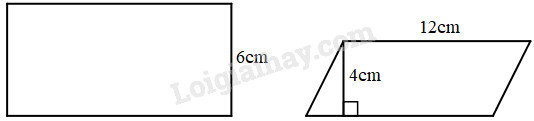
A. 48cm B. 14cm C. 28cm D. 32cm
Phương pháp giải:
Áp dụng các quy tắc:
- Muốn tính diện tích hình bình hành ta lấy độ dài đáy nhân với chiều cao tương ứng với đáy.
- Muốn tính chiều dài hình chữ nhật ta lấy diện tích chia cho chiều rộng.
- Muốn tính chu vi hình chữ nhật ta lấy chiều dài cộng với chiều rộng rồi nhân với 2.
Lời giải chi tiết:
Diện tích hình bình hành đó là:
\(12 \times 4 = 48\,\,(c{m^2})\)
Vì hình chữ nhật và hình bình hành có diện tích bằng nhau nên hình chữ nhật có diện tích là \(48c{m^2}\).
Chiều dài của hình chữ nhật là:
\(48:6 = 8\,\,(cm)\)
Chu vi hình chữ nhật đó là:
\((8 + 6) \times 2 = 28\,\,(cm)\)
Đáp số: \(28cm\).
Chọn C.
Bài 9
Viết tiếp vào chỗ chấm cho thích hợp:
Biểu đồ dưới đây nói về diện tích của ba vườn quốc gia:
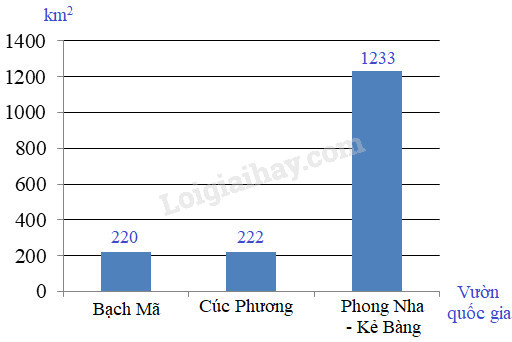
a) Theo biểu đồ trên, vườn quốc gia có diện tích nhỏ nhất là: ……
b) Diện tích vườn quốc gia Phong Nha – Kẻ Bàng nhiều hơn diện tích vườn quốc gia Cúc Phương là …… km2.
Phương pháp giải:
- Quan sát biểu đồ để tìm diện tích của mỗi vườn quốc gia, sau đó so sánh các diện tích để tìm vườn quốc gia có diện tích nhỏ nhất.
- Muốn biết diện tích vườn quốc gia Phong Nha – Kẻ Bàng nhiều hơn diện tích vườn quốc gia Cúc Phương bao nhiêu ki-lô-mét vuông ta lấy diện tích vườn quốc gia Phong Nha – Kẻ Bàng trừ đi diện tích vườn quốc gia Cúc Phương.
Lời giải chi tiết:
a) Quan sát biểu đồ ta thấy: diện tích vườn quốc gia Bạch Mã là \(220k{m^2}\); diện tích vườn quốc gia Cúc Phương là \(222k{m^2}\); diện tích vườn quốc gia Phong Nha – Kẻ Bàng là \(1233k{m^2}\).
Mà \(220k{m^2} < 222k{m^2} < 1233k{m^2}\).
Vậy vườn quốc gia có diện tích nhỏ nhất là Bạch Mã.
b) Diện tích vườn quốc gia Phong Nha – Kẻ Bàng nhiều hơn diện tích vườn quốc gia Cúc Phương số ki-lô-mét vuông là:
\(1233 - 222 = 1011\,\,(k{m^2})\)
Bài 10
Giải bài toán:
Ba đội sửa đường, đội 1 sửa được đoạn đường dài 4850m, đội 2 sửa được đoạn đường bằng \(\dfrac{4}{5}\) đoạn đường của đội 1, đội 3 sửa được đoạn đường bằng mức trung bình của đội 1 và đội 2. Hỏi đội 3 sửa đoạn đường dài bao nhiêu mét?
Phương pháp giải:
- Tính độ dài đoạn đường đội 2 sửa được ta lấy độ dài đoạn đường đội 1 sửa được nhân với \(\dfrac{4}{5}\), hay lấy \(4850m\) nhân với \(\dfrac{4}{5}\).
- Tính độ dài đoạn đường đội 3 sửa được ta lấy tổng độ dài đoạn đường đội 1 và đội 2 sửa được chia cho 2.
Lời giải chi tiết:
Đội 2 sửa được đoạn đường dài số mét là:
\(4850 \times \dfrac{4}{5} = 3880\;(m)\)
Đội 3 sửa được đoạn đường dài số mét là:
\((4850 + 3880):2 = 4365\;(m)\)
Đáp số: \(4365m\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải câu 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 trang 64, 65, 66 timdapan.com"







