Giải câu hỏi trắc nghiệm trang 77, 78 vở thực hành Toán 9
Cho tam giác PQR như Hình 4.12. Khi đó ta có: A. (PQ = PR.sin P). B. (PQ = PR.cos R). C. (QR = PR.cos P). D. (QR = PR.cos R).
Chọn phương án đúng trong mỗi câu sau:
Câu 1
Trả lời Câu 1 trang 77 Vở thực hành Toán 9
Cho tam giác PQR như Hình 4.12. Khi đó ta có:
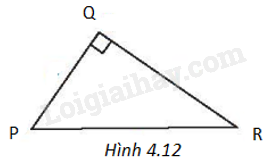
A. \(PQ = PR.\sin P\).
B. \(PQ = PR.\cos R\).
C. \(QR = PR.\cos P\).
D. \(QR = PR.\cos R\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác PQR vuông tại Q nên \(PQ = PR.\cos P = PR.\sin R\), \(QR = PR.\cos R\)
Chọn D
Câu 2
Trả lời Câu 1 trang 77 Vở thực hành Toán 9
Cho tam giác PQR như Hình 4.12. Khi đó
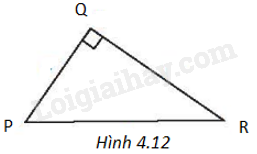
A. \(PQ = QR.\tan P\).
B. \(PQ = QR.\cot R\).
C. \(QR = PQ.\tan P\).
D. \(QR = PQ.\cot P\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết:
Vì tam giác PQR vuông tại Q nên \(PQ = QR.\tan R = QR.\cot P\), \(QR = PQ.\tan P = PQ.\cot R\)
Chọn C
Câu 3
Trả lời Câu 3 trang 77 Vở thực hành Toán 9
Cho tam giác vuông MNP như Hình 4.13. Khi đó
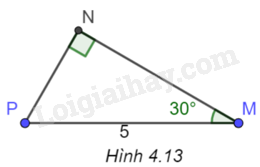
A. \(MN = \frac{5}{2}\).
B. \(MN = \frac{{5\sqrt 3 }}{3}\).
C. \(MN = 5\sqrt 3 \).
D. \(MN = \frac{{5\sqrt 3 }}{2}\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác MNP vuông tại N nên
\(MN = PM.\cos M = 5.\cos {30^o} = \frac{{5\sqrt 3 }}{2}\)
Chọn D
Câu 4
Trả lời Câu 4 trang 78 Vở thực hành Toán 9
Cho tam giác vuông MNP như Hình 4.14. Tìm khẳng định sai trong các khẳng định sau?
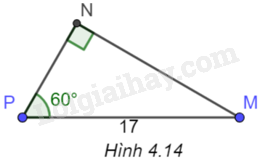
A. \(NP = 8,5\).
B. \(MN = \frac{{17\sqrt 3 }}{2}\).
C. \(NP = MN.\tan {60^o}\).
D. \(NP = MN.\cot {60^o}\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
Vì tam giác MNP vuông tại N nên:
+ \(NP = PM.\cos P = 17.\cos {60^o} = 8,5\)
+ \(MN = PM.\sin P = 17.\sin {60^o} = \frac{{17\sqrt 3 }}{2}\)
+ \(NP = MN.\tan M = MN.\tan \left( {{{90}^o} - {{60}^o}} \right) \) \(= MN.\tan {30^o};\)
\(NP = MN.\cot P = MN.\cot {60^o}\)
Chọn C
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải câu hỏi trắc nghiệm trang 77, 78 vở thực hành Toán 9 timdapan.com"







