Giải bài tập 5 trang 79 SGK Toán 9 tập 2 - Cánh diều
Cho tứ giác ABCD và các điểm M, N lần lượt thuộc các đoạn thẳng AB và CD sao cho các tứ giác AMND, BMNC là các tứ giác nội tiếp. Chứng minh \(\widehat A + \widehat B = 180^\circ .\)
Đề bài
Cho tứ giác ABCD và các điểm M, N lần lượt thuộc các đoạn thẳng AB và CD sao cho các tứ giác AMND, BMNC là các tứ giác nội tiếp. Chứng minh \(\widehat A + \widehat B = 180^\circ .\)
Phương pháp giải - Xem chi tiết
Áp dụng tính chất: Hình chữ nhật có 2 đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường để chứng minh AO = CO = OB = OD = R.
Lời giải chi tiết
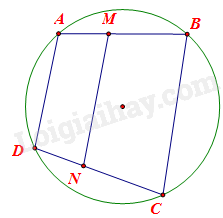
Do AMND nội tiếp nên \(\widehat A + \widehat {MND} = 180^\circ \) (1) và MBCN nội tiếp nên \(\widehat B + \widehat {MNC} = 180^\circ \left( 2 \right).\)
Ta lại có \(\widehat {MND} + \widehat {MNC} = 180^\circ \)(kề bù) (3)
Cộng vế với vế của (1), (2), và kết hợp với (3) ta có:
\(\begin{array}{l}\widehat A + \widehat {MND} + \widehat {MNC} + \widehat B = 180^\circ + 180^\circ = 360^\circ \\\widehat A + \widehat B = 360^\circ - \left( {\widehat {MND} + \widehat {MNC}} \right)\\\widehat A + \widehat B = 360^\circ - 180^\circ = 180^\circ \end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 5 trang 79 SGK Toán 9 tập 2 - Cánh diều timdapan.com"







