Giải bài tập 3 trang 74 SGK Toán 9 tập 2 - Cánh diều
Cho bán kính đường tròn nội tiếp tam giác đều bằng 4cm. Tính cạnh của tam giác đều đó.
Đề bài
Cho bán kính đường tròn nội tiếp tam giác đều bằng 4cm. Tính cạnh của tam giác đều đó.
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng tính chất đường trung tuyến của tam giác để tính EI.
Bước 2: Biểu diễn FI theo FG và EF.
Bước 3: Áp dụng định lý Pytago trong tam giác EFI để tính cạnh EF.
Lời giải chi tiết
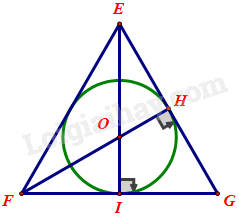
Gọi (O; OI) là đường tròn nội tiếp tam giác đều EFG nên O là giao của đường trung trực EI, FH; và OI = 4cm.
EI là đường trung trực của tam giác đều EFG nên \(FI = \frac{{FG}}{2} = \frac{{EF}}{2}\) và EI đồng thời là đường trung tuyến do đó \(EI = 3OI = 3.4 = 12cm.\)
Áp dụng định lý Pytago trong tam giác EFI vuông tại I:
\(\begin{array}{l}E{F^2} = E{I^2} + F{I^2}\\E{F^2} = {12^2} + {\frac{{EF}}{4}^2}\\\frac{{3E{F^2}}}{4} = 144\\EF = 8\sqrt 3 cm.\end{array}\)
Vậy cạnh của tam giác đều là \(8\sqrt 3 cm.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 3 trang 74 SGK Toán 9 tập 2 - Cánh diều timdapan.com"







