Giải bài tập 1.11 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) \(y = {x^4} - 2{x^2} + 3\); b) \(y = x.{e^{ - x}}\); c) \(y = x\ln x\); d) \(y = \sqrt {x - 1} + \sqrt {3 - x} \).
Đề bài
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = {x^4} - 2{x^2} + 3\);
b) \(y = x.{e^{ - x}}\);
c) \(y = x\ln x\);
d) \(y = \sqrt {x - 1} + \sqrt {3 - x} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn để tính: Giả sử \(y = f\left( x \right)\) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm \(f'\left( x \right) = 0\).
Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {a;b} \right]\):
1. Tìm các điểm \({x_1},{x_2},...{x_n} \in \left( {a;b} \right)\), tại đó \(f'\left( x \right) = 0\) hoặc không tồn tại.
2. Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right)\), f(a) và f(b).
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.
Ta có: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\)
Lời giải chi tiết
a) \(y = {x^4} - 2{x^2} + 3\)
\(y' = 4{x^3} - 4x,y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\)
\(y\left( 0 \right) = 3;y\left( 1 \right) = y\left( { - 1} \right) = 2\)
Do đó, \(\mathop {\max }\limits_{\left( { - \infty ; + \infty } \right)} y = y\left( 0 \right) = 3,\mathop {\min }\limits_{\left( { - \infty ; + \infty } \right)} y = y\left( 1 \right) = y\left( { - 1} \right) = 2\)
b) Ta có: \(y' = {e^{ - x}} - x.{e^{ - x}},y' = 0 \Leftrightarrow {e^{ - x}} - x.{e^{ - x}} = 0 \Leftrightarrow {e^{ - x}}\left( {1 - x} \right) = 0 \Leftrightarrow x = 1\)
Bảng biến thiên:
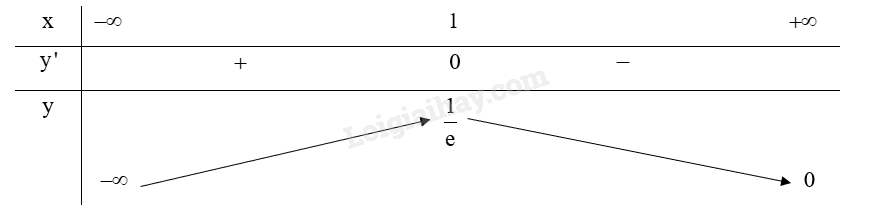
Do đó, \(\mathop {\max }\limits_{\left( { - \infty ; + \infty } \right)} y = y\left( 1 \right) = \frac{1}{e}\), hàm số không có giá trị nhỏ nhất.
c) Tập xác định của hàm số là: \(D = \left( {0; + \infty } \right)\)
\(y' = \ln x + x.\frac{1}{x} = \ln x + 1,y' = 0 \Leftrightarrow \ln x + 1 = 0 \Leftrightarrow x = \frac{1}{e}\) (thỏa mãn)
Bảng biến thiên:

Hàm số không có giá trị lớn nhất, \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = y\left( {\frac{1}{e}} \right) = \frac{{ - 1}}{e}\)
d) Tập xác định của hàm số là \(\left[ {1;3} \right]\).
\(y' = \frac{1}{{2\sqrt {x - 1} }} - \frac{1}{{2\sqrt {3 - x} }},y' = 0 \Leftrightarrow \frac{1}{{2\sqrt {x - 1} }} - \frac{1}{{2\sqrt {3 - x} }} = 0 \Leftrightarrow \frac{{\sqrt {3 - x} - \sqrt {x - 1} }}{{2\sqrt {3 - x} \sqrt {x - 1} }} = 0\)
\( \Leftrightarrow \sqrt {3 - x} = \sqrt {x - 1} \Leftrightarrow 3 - x = x - 1 \Leftrightarrow x = 2\left( {tm} \right)\)
\(y\left( 1 \right) = \sqrt 2 ;y\left( 2 \right) = 2;y\left( 3 \right) = \sqrt 2 \)
Do đó, \(\mathop {\max }\limits_{\left[ {1;3} \right]} y = y\left( 2 \right) = 2,\mathop {\min }\limits_{\left[ {1;3} \right]} y = y\left( 1 \right) = y\left( 3 \right) = \sqrt 2 \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 1.11 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức timdapan.com"







