Giải bài tập 1.1 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau: a) Đồ thị hàm số (y = {x^3} - frac{3}{2}{x^2}) (H.1.11); b) Đồ thị hàm số (y = sqrt[3]{{{{left( {{x^2} - 4} right)}^2}}}) (H.1.12).
Đề bài
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
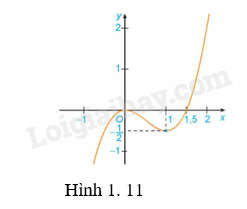
a) Đồ thị hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) (H.1.11);
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
a) Đồ thị hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) (H.1.11);
b) Đồ thị hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) (H.1.12).

Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến của hàm số:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải chi tiết
a) Hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) đồng biến trên \(\left( { - \infty ;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) nghịch biến trên \(\left( {0;1} \right)\).
b) Hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) đồng biến trên \(\left( { - 2;0} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( {0;2} \right)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 1.1 trang 13 SGK Toán 12 tập 1 - Kết nối tri thức timdapan.com"







