Bài IV.10* trang 56 SBT Vật Lí 11

Đề bài

Hai dòng điện cường độ 2,0 A và 4,0 A chạy trong hai dây dẫn thẳng dài, đồng phẳng và được đặt vuông góc với nhau trong không khí. Xác định :

a) Cảm ứng từ tại những điểm nằm trong mặt phẳng chứa hai dòng điện và cách đều hai dây dẫn các khoảng cách r= 4,0 cm.

b) Quỹ tích các điểm nằm trong mặt phẳng chứa hai dòng điện tại đó cảm ứng từ có giá trị bằng không.

Lời giải chi tiết

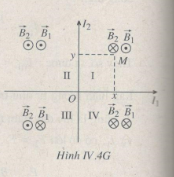
Gọi \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) là các vectơ cảm ứng từ do dòng điện I₁ và I₂  gây ra trong từ trường của chúng. Trong mặt phẳng chứa hai dòng điện I₁ và I₂ có bốn góc vuông (Hình IV.4G) : hai góc vuông I và III ứng với \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \)  cùng phương ngược chiểu, hai góc vuông II và IV ứng với \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \)  cùng phương cùng chiều. Đồng thời, tại một điểm M (x, y) nằm trong mặt phẳng chứa I₁ và I₂, các vectơ  và  có độ lớn bằng :

\({B_1} = 2.10^{ - 7}{\dfrac{I_1}{y}};{B_2} = 2.10^{ - 7}{\dfrac{I_2}{x}}\)

a) Tại điểm M (x,y) cách đều hai dây dẫn: x = y = r – 4,0 cm, ta có:

\({B_1} = {2.10^{ - 7}}.{\dfrac{2,0}{4,0.10^{ - 2}}} = {1,0.10^{ - 5}}T\) 

\( {B_2} = {2.10^{ - 7}}.{\dfrac{4,0}{4,0.10^{ - 2}}} = 2,0.10^{ - 5}T\)

Khi đó, cảm ứng từ tổng hợp tại điểm M(x, y) có giá trị bằng:

\(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)

- Nếu điểm M(x,y) nằm tại các góc vuông I và III, thì:

\(B = B_2– B_1 = 2,0.10^{-5} – 1,0.10^{-5} = 1,0.10^{-5}T\)

- Nếu điểm M(x,y) nằm tại các góc vuống II và IV thì:

\(B = B_2 + B_1 = 2,0.10^{-5} + 1,0.10^{-5}= 3.1,0.10^{-5}T\)

b) Quỹ tích của những điểm tại đó cảm ứng từ \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} = \overrightarrow 0 \) phải nằm trong hai góc vuông I và III ứng với \(\overrightarrow {{B_1}} \) và \(\overrightarrow {{B_2}} \) cùng phương ngược chiều sao cho:

 \({B_1} = {B_2} \Rightarrow {\dfrac{I_1}{y}} = {\dfrac{I_2}{x}} \Rightarrow y = {\dfrac{2,0}{4,0}}x = \dfrac{x}{2}\)

Như vậy quỹ tích phải tìm là đường thẳng \(y = \dfrac{x}{2}\) trừ điểm O.