Bài 89 trang 78 Vở bài tập toán 6 tập 2

Đề bài

Tỉ số của hai số \(a\) và \(b\) bằng \(1\dfrac{1}{2}\) . Tìm hai số đó biết \(a - b = 8\)

Lời giải chi tiết

Ta có \(1\dfrac{1}{2} = \dfrac{3}{2}\). Như vậy theo đề bài thì \(a:b=3:2\).

Ta có sơ đồ 

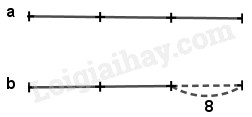
Theo sơ đồ, ta tính được : 

\(a=8\times3=24\); \(b=8\times2=16\)

Lưu ý 

Bài này có thể giải theo nhiều cách khác. Sau đây là ba cách giải nữa.

Cách 1. \(\dfrac{a}{b} = \dfrac{3}{2}\) nên \(a = \dfrac{{3}}{2}.b\). Do đó, \(a - b = \dfrac{3}{2}b - b = \left( {\dfrac{3}{2} - 1} \right) \cdot b\)\( = \dfrac{1}{2}b.\)

Vì \(a - b = 8\) nên \(\dfrac{1}{2}b = 8\), suy ra :

\(b = 8:\dfrac{1}{2} = 16;a = \dfrac{3}{2} \cdot b = \dfrac{3}{2} \cdot 16 = 24\)

Cách 2. \(\dfrac{a}{b} = \dfrac{3}{2}\) nên \(b = \dfrac{{2}}{3}.a\). Do đó, \(a - b = a-\dfrac{2}{3}a = \left( {1-\dfrac{2}{3}} \right) \cdot a\)\( = \dfrac{1}{3}a.\)

Vì \(a - b = 8\) nên \(\dfrac{1}{3}a = 8\), suy ra :

\(a = 8:\dfrac{1}{3} = 24;b = \dfrac{2}{3} \cdot a = \dfrac{2}{3} \cdot 24 = 16\).

Cách 3. \(\dfrac{a}{b} = \dfrac{3}{2}\) nên \(a=3.k,b=2.k\) \(\left( {k \in Z,k \ne 0} \right).\)

Vì \(a - b = 8\) suy ra \(3.k-2.k=8\) hay \(k=8\).

Vậy \(a=3.k=3.8=24\), \(b=2.k=2.8=16\).