Giải bài 8 trang 65 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.
Đề bài
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
+ Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Lời giải chi tiết
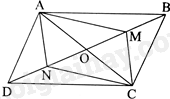
Tứ giác ABCD là hình bình hành nên \(OA = OC\), \(OB = OD\)
Mà: \(ON = \frac{1}{2}OD\) (do N là trung điểm của OD)
\(OM = \frac{1}{2}OB\) (do M là trung điểm của OB)
Do đó, \(OM = ON\)
Tứ giác AMCN có: \(OM = ON\) (cmt), \(OA = OC\) (cmt) nên tứ giác AMCN là hình bình hành.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 8 trang 65 sách bài tập toán 8 - Chân trời sáng tạo timdapan.com"







