Giải bài 1 trang 65 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.
Đề bài
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Trong hình bình hành:
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.
+ Hai cạnh đối song song với nhau.
Lời giải chi tiết
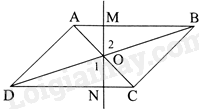
Vì ABCD là hình bình hành (gt) nên \(OB = OD\), AB//CD. Do đó, \(\widehat {OBM} = \widehat {ODN}\) (hai góc so le trong)
Tam giác OBM và tam giác ODN có:
\(\widehat {OBM} = \widehat {ODN}\)(cmt), \(OB = OD\) (cmt), \(\widehat {BOM} = \widehat {NOD}\) (hai góc đối đỉnh).
Do đó, \(\Delta OBM = \Delta ODN\left( {g - c - g} \right)\)
Suy ra \(OM = ON\). Vậy O là trung điểm của MN
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 1 trang 65 sách bài tập toán 8 - Chân trời sáng tạo timdapan.com"







