Giải bài 8 trang 57 SGK Toán 10 tập 1 – Chân trời sáng tạo
Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.
Đề bài
Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.
Phương pháp giải - Xem chi tiết
Gọi công thức của hàm số bậc hai là \(y = a{x^2} + bx + c\)
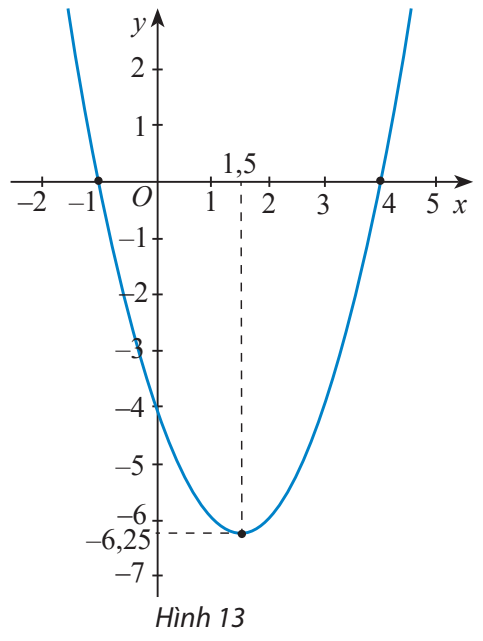
Đồ thị hàm số đi qua 3 điểm có tọa độ (-1;0), (4;0), (0;-4)
Lời giải chi tiết
Gọi công thức của hàm số bậc hai là \(y = a{x^2} + bx + c\)
Đồ thị hàm số đi qua 3 điểm có tọa độ (-1;0), (4;0), (0;-4)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}a.{( - 1)^2} + b.( - 1) + c = 0\\a{.4^2} + b.4 + c = 0\\a{.0^2} + b.0 + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b + c = 0\\16a + 4b + c = 0\\c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b = 4\\16a + 4b = 4\\c = - 4\end{array} \right.\\ \Leftrightarrow a = 1,b = - 3,c = - 4.\end{array}\)
Vậy hàm số cần tìm có công thức \(y = {x^2} - 3x - 4\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 8 trang 57 SGK Toán 10 tập 1 – Chân trời sáng tạo timdapan.com"







