Bài 77 trang 114 SBT toán 9 tập 2
Giải bài 77 trang 114 sách bài tập toán 9. Tính diện tích phần gạch sọc trên hình sau (theo kích thước đã cho trên hình)...
Đề bài
Tính diện tích phần gạch sọc trên hình sau (theo kích thước đã cho trên hình)
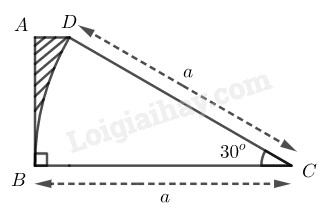
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng cạnh huyền nhân với \(\sin\) góc đối hoặc \(\cos\) góc kề.
+) Diện tích hình thang bằng nửa tổng hai đáy nhân với chiều cao.
+) Diện tích hình quạt tròn bán kính \(R,\) cung \(n^\circ\) được tính theo công thức: \(S=\dfrac{\pi R^2n}{360}.\)
Lời giải chi tiết
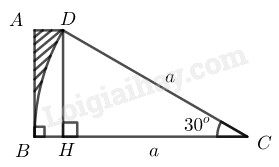
Diện tích phần gạch sọc là hiệu giữa diện tích hình thang \(ABCD\) và diện tích hình quạt tròn có góc ở tâm \(30^0\) của đường tròn bán kính bằng a.
Từ \(D\) kẻ \(DH \bot BC\), suy ra \(ADHB\) là hình chữ nhật.
Trong tam giác vuông \(HDC\) có \(\widehat {DHC} = {90^0}\)
\(DH = DC.\sin \widehat{C} = a.\sin {30^0} = \displaystyle{a \over 2}\)
\(CH = DC.\cos\widehat C = a.\cos{30^0} =\displaystyle {{a\sqrt 3 } \over 2}\)
\(BH = BC - HC = \displaystyle a - {{a\sqrt 3 } \over 2} \)\(= \displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2}\)
\( \Rightarrow AD =BH= \displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2}\) (do \(ADHB\) là hình chữ nhật)
Diện tích của hình thang \(ABCD\) bằng:
\(\displaystyle{{AD + BC} \over 2}.DH \)\(=\displaystyle{{\displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2} + a} \over 2}.{a \over 2}\)
\( = \displaystyle {{{a^2}\left( {4 - \sqrt 3 } \right)} \over 8}\)
Diện tích hình quạt tròn bằng: \(\displaystyle{{\pi .{a^2}.30} \over {360}} = {{\pi {a^2}} \over {12}}\)
Diện tích phần gạch sọc:
\(S = \displaystyle{{{a^2}\left( {4 - \sqrt 3 } \right)} \over 8} - {{\pi a} \over {12}}\)
\( = \displaystyle{{3{a^2}\left( {4 - \sqrt 3 } \right) - 2\pi {a^2}} \over {24}}\)
\( = \displaystyle{{{a^2}} \over {24}}\left( {12 - 3\sqrt 3 - 2\pi } \right)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 77 trang 114 SBT toán 9 tập 2 timdapan.com"







