Bài 3.12 phần bài tập bổ sung trang 116 SBT toán 9 tập 2
Giải bài 3.12 phần bài tập bổ sung trang 116 sách bài tập toán 9. Cho hình như hình bên (PQ = PR; QY và RX là các tia phân giác). Khi đó, PYKX là:...
Đề bài
Cho hình như hình bên \((PQ = PR;\) \(QY\) và \(RX\) là các tia phân giác\().\) Khi đó, \(PYKX\) là:
\((A)\) hình thang và không phải là hình bình hành.
\((B)\) hình bình hành và không phải hình thoi.
\((C)\) hình thoi và không phải hình chữ nhật.
\((D)\) hình chữ nhật.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Tứ giác có các góc đối bằng nhau là hình bình hành.
+) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
+) Hình chữ nhật là tứ giác có \(4\) góc vuông.
Lời giải chi tiết
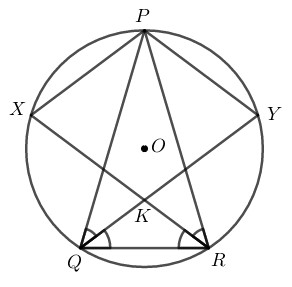
Ta có: \(PQ=PR\) (gt) nên tam giác \(PQR\) cân tại P
Suy ra \( \widehat{PQR}=\widehat{PRQ}\)
Mà \(QY,RX\) lần lượt là tia phân giác của các góc \( \widehat{PQR},\widehat{PRQ}\)
Nên \( \widehat{PQY}=\widehat{YQR}\)\(= \widehat{QRX}=\widehat{XRP}\)
Suy ra các cung \(PX,PY,QX,RY\) bằng nhau (các góc nội tiếp bằng nhau chắn các cung bằng nhau)
Suy ra \( \widehat{PRX}=\widehat{RPY}\) (hai góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Mà hai góc ở vị trí so le trong nên \(XR//PY\)
Lại có \( \widehat{PQY}=\widehat{XPQ}\) (hai góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Mà hai góc ở vị trí so le trong nên \(PX//QY\)
Suy ra tứ giác \(PXKY\) là hình bình hành.
Mà \(PX=PY\) (do cung PX bằng cung PY) nên \(PXKY\) là hình thoi.
Mặt khác: \(\widehat{PXR}\ne 90^\circ\) (vì \(PQ\) không phải đường kính)
Do đó: tứ giác \(PXKY\) là hình thoi nhưng không phải hình chữ nhật.
Vậy chọn \((C)\) hình thoi và không phải hình chữ nhật.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3.12 phần bài tập bổ sung trang 116 SBT toán 9 tập 2 timdapan.com"







