Bài 6 trang 89 Vở bài tập toán 9 tập 2

Đề bài

Trên đường tròn tâm \(O\) lấy ba điểm \(A, B, C\) sao cho \(\widehat {AOB} = {100^o}\) . Số đo cung \(AC\) bằng \(45\)^o. Tính số đo cung nhỏ \(BC\) và cung lớn \(BC\) (xét cả hai trường hợp: điểm \(C\) nằm trên cung nhỏ \(AB\), điểm \(C\) nằm trên cung lớn \(AB\)).

Lời giải chi tiết

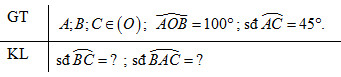
a) Điểm \(C\) nằm trên cung nhỏ \(AB.\)

sđ\(\overparen{BC}=\) sđ\(\overparen{AB}-\) sđ\(\overparen{AC}\)\( = 100^\circ  - 45^\circ  = 55^\circ \)

sđ\(\overparen{BAC}= 360^\circ  - 55^\circ  = 305^\circ \)

b) Điểm \(C\) nằm trên cung lớn \(AB.\)

sđ\(\overparen{BAC}=\) sđ\(\overparen{AC}+\) sđ\(\overparen{AB}\)\( = 100^\circ  + 45^\circ  = 145^\circ \)

sđ\(\overparen{BC}= 360^\circ  - 145^\circ  = 215^\circ \)