Bài 2 trang 87 Vở bài tập toán 9 tập 2

Đề bài

Cho hai đường thằng \(xy\) và \(st\) cắt nhau tại \(O\), trong các góc tạo thành có góc \(40\)^o. Vẽ một đường tròn tâm \(O\). Tính số đo góc ở tâm xác định bởi hai trong bốn tia gốc \(O\).

Lời giải chi tiết

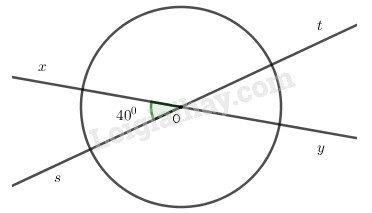
Ta có \(\widehat {xOs} = 40^\circ \) , suy ra \(\widehat {yOt} = \widehat {xOt} = 40^\circ \) (hai góc đối đỉnh)

Khi đó, ta có \(\widehat {xOt} = 180^\circ  - \widehat {xOs} = 180^\circ  - 40^\circ\)\(  = 140^\circ \) (hai góc kề bù)  

Suy ra \(\widehat {yOs} = \widehat {xOt} = 140^\circ \) vì hai góc đối đỉnh

Vậy ta có:\(\widehat {xOt} = \widehat {sOy} = 140^\circ ;\)\(\widehat {xOs} = \widehat {tOy} = 40^\circ .\)