Bài 5 trang 88 Vở bài tập toán 9 tập 2

Đề bài

Cho tam giác đều \(ABC\). Gọi \(O\) là tâm của đường tròn đi qua ba đỉnh \(A, B, C\)

a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính \(OA, OB, OC\)

b) Tính số đo các cung tạo bởi hai trong ba điểm \(A, B, C\)

Lời giải chi tiết

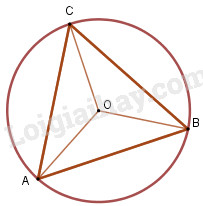
a) Từ giả thiết ta có \(\Delta AOC = \Delta AOB = \Delta COB\) (c - c - c)

suy ra \(\widehat {AOC} = \widehat {BOC} = \widehat {AOB}\)  (các góc tương ứng)

mà \(\widehat {ACB}=60^0\)\(  \Rightarrow \widehat {AOB} = \widehat {AOC} = \widehat {BOC} \)\( = 120^\circ \)

b) Từ câu a) suy ra sđ\(\overparen{AC}=\overparen{BC}=\overparen{AB}\)\( = 120^\circ \)

Suy ra sđ\(\overparen{ABC}\) = sđ\(\overparen{BAC}\) = sđ\(\overparen{ACB}\) \( = 360^\circ  - 120^\circ  = 240^\circ \)