Giải Bài 6 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.
Đề bài
Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.
a) Chứng minh rằng \(\Delta \)MFN = \(\Delta \)PFD
b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của GH. Gọi K là trung điểm của GK. Chứng minh rằng ba điểm M, H, K thẳng hàng.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta \)MFN = \(\Delta \)PFD theo trường họp cạnh góc cạnh
Sử dụng tính chất của điểm đối xứng qua một điểm, trung điểm của 1 đoạn thẳng và 2 góc đối đỉnh
b) Chứng minh H là trọng tâm của tam giác MPD sau đó dựa vào tính chất ta suy ra M, H, K thẳng hàng
Lời giải chi tiết
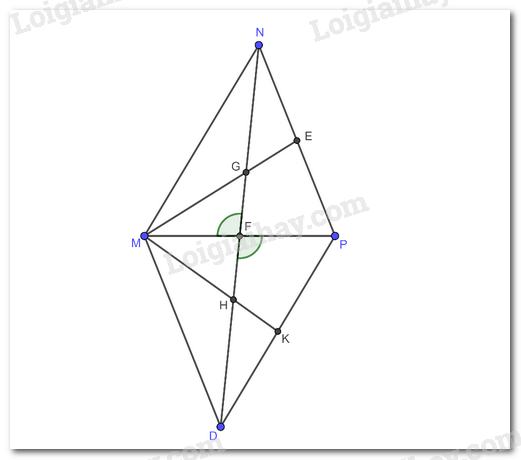
a) Vì N đối xứng với D qua F (theo giả thiết)
Nên NF = DF (1)
Vì F là trung điểm của MP (theo giả thiết)
Nên MF = PF (2)
Vì góc NFM và góc PFD ở vị trí đối đỉnh nên 2 góc bằng nhau (3)
Từ (1), (2) và (3) \( \Rightarrow \)\(\Delta \)MFN = \(\Delta \)PFD (c-g-c)
b) Xét tam giác MPD có :
F là trung điểm MD,
K là trung điểm DP (theo giả thiết)
Mà 2 đường trung tuyến của tam giác MPD là DF và MK cắt nhau tại H
\( \Rightarrow \) H là trọng tâm \(\Delta \)MPD
\( \Rightarrow \) M, H, K thẳng hàng
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 6 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo timdapan.com"







