Bài 52 trang 46 SBT toán 7 tập 2
Giải bài 52 trang 46 sách bài tập toán 7. Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng ba điểm B, I, K thẳng hàng.
Đề bài
Cho tam giác \(ABC.\) Các tia phân giác các góc \(A\) và \(C\) cắt nhau ở \(I.\) Các đường phân giác các góc ngoài tại đỉnh \(A\) và \(C\) cắt nhau ở \(K.\) Chứng minh rằng ba điểm \(B, I, K\) thẳng hàng.
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Tính chất đường phân giác của góc: Các điểm nằm trên đường phân giác của một góc cách đều hai cạnh của góc đó.
+) Điểm cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Lời giải chi tiết
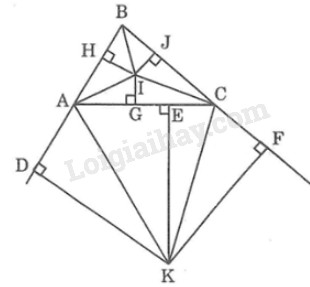
Kẻ \(IH \bot AB,IJ \bot BC,IG \bot AC\),
\(KD \bot AB,KE \bot AC,KF \bot BC\)
Vì \(I\) nằm trên tia phân giác của \(\widehat {BAC}\)
\( \Rightarrow IH = IG \) (tính chất tia phân giác)
Vì \(I\) nằm trên tia phân giác của \(\widehat {BCA}\)
\( \Rightarrow IG = IJ\) (tính chất tia phân giác)
Suy ra: \( IH = IJ\)
Nên \(I\) nằm trên tia phân giác của \(\widehat {ABC}\) (1)
Vì \(K\) nằm trên tia phân giác của \(\widehat {DAC}\)
\( \Rightarrow KD = KE\) (tính chất tia phân giác)
Vì \(K\) nằm trên tia phân giác của \(\widehat {ACF}\)
\( \Rightarrow KE = KF\) (tính chất tia phân giác)
Suy ra: \(KD = KF \Rightarrow K\) nằm trên tia phân giác của \(\widehat {ABC}\) (2)
Từ (1) và (2) suy ra: \(B, I, K\) thẳng hàng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 52 trang 46 SBT toán 7 tập 2 timdapan.com"







