Bài 5.1, 5.2, 5.3, 5.4, 5.5 phần bài tập bổ sung trang 45, 46 SBT toán 7 tập 2

Bài 5.1

Cho góc \(xOy\) bằng \(60°,\) điểm \(M\) nằm trong góc đó và cùng cách \(Ox, Oy\) một khoảng bằng \(2cm.\) Khi đó đoạn thẳng \(OM\) bằng

(A) \(2cm;\)               (B) \(3cm;\)

(C) \(4cm;\)               (D) \(5cm\)

Hãy chọn phương án đúng.

Phương pháp giải:

Sử dụng: 

+) Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó

+) Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

+) Nếu tam giác vuông có một góc nhọn bằng \(30^0\) thì cạnh góc vuông đối diện với góc nhọn đó bằng nửa cạnh huyền

Lời giải chi tiết:

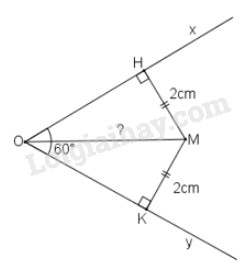
Do \(M\) cùng cách \(Ox, Oy\) những khoảng bằng nhau nên \(M\) nằm trên tia phân giác của góc \(xOy.\)

Gọi \(H\) là chân đường vuông góc kẻ từ \(M\) đến \(Ox \) thì tam giác vuông \(HOM\) có \(HM=2cm\) và \(\widehat {HOM} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\)

Nên \(MH=OM:2\) (Nếu tam giác vuông có một góc nhọn bằng \(30^0\) thì cạnh góc vuông đối diện với góc nhọn đó bằng nửa cạnh huyền)

Hay \(OM = 2MH = 4cm\)

Chọn (C)

Bài 5.2

Cho điểm \(A\) nằm trong góc vuông \(xOy.\) Gọi \(M, N \) lần lượt là chân đường vuông góc kẻ từ \(A\) đến \(Ox, Oy.\) Biết \(AM = AN = 3cm.\) Khi đó

(A) \(OM = ON > 3cm \)

(B) \(OM = ON < 3cm\)

(C) \(OM = ON = 3cm \)

(D) \(OM \ne ON\)

Phương pháp giải:

Sử dụng: 

+) Hình vuông có bốn cạnh bằng nhau

+) Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó

+) Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

Lời giải chi tiết:

+) Vì A nằm trong góc xOy và cách đều Ox, Oy (do AM = AN = 3cm) nên điểm A nằm trên tia phân giác của góc xOy.

Suy ra: OA là tia phân giác của góc xOy.

Do đó: \(\widehat {MOA} = \widehat {NOA} = \dfrac{{\widehat {MON}}}{2} \)\(= \dfrac{{{{90}^0}}}{2} = {45^0}\)

Tam giác \(MAO\) vuông tại M có \(\widehat {MOA}=45^0\) nên \(\widehat {MAO}=90^0-45^0=45^0\)

Do đó, tam giác \(MAO\) vuông cân tại \(M,\) bởi vậy \(MO = MA = 3cm.\)

+) Chứng minh tương tự ta có tam giác OAN vuông cân tại N nên (NO = NA = 3cm.\)

Vậy \(OM=ON=3cm\)

Chọn (C)

Bài 5.3

Cho góc đỉnh \(O\) khác góc bẹt.

a) Từ một điểm \(M\) trên tia phân giác của góc \(O,\) kẻ các đường vuông góc \(MA, MB\) đến hai cạnh của góc này. Chứng minh rằng \(AB \bot OM\)

b) Trên hai cạnh của góc \(O\) lấy hai điểm \(C\) và \(D,\) sao cho \(OC = OD.\) Hai đường thẳng lần lượt vuông góc với hai cạnh của góc \(O\) tại \(C\) và \(D\) cắt nhau ở \(E.\) Chứng minh rằng \(OE\) là tia phân giác của góc \(O.\)

Phương pháp giải:

Sử dụng: 

+) Tính chất hai tam giác bằng nhau

+) Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó

+) Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

Lời giải chi tiết:

a) 

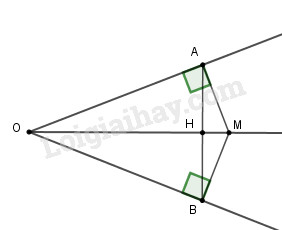
Gọi \(H\) là giao điểm của \(AB\) và \(OM.\)

Xét hai tam giác vuông \(AOM\) và \(BOM,\) ta có:

+) Cạnh huyền \(OM\) chung

+) \(MA = MB\) (vì \(M\) thuộc tia phân giác của góc \(O).\)

Vậy \(∆AOM = ∆BOM\) (cạnh huyền - cạnh góc vuông).

Suy ra  \(OA = OB.\)

Từ đó, xét \(∆AOH\) và \(∆BOH\) có:

+) \(OA=OB\) (cmt)

+) \(\widehat {AOH} = \widehat {BOH}\) (vì \(OH\) là phân giác góc \(O)\)

+) \(OH\) là cạnh chung

Nên \(∆AOH = ∆BOH\) (c.g.c). Suy ra \(\widehat {AHO} = \widehat {BHO} \)

Mà \(\widehat {AHO} + \widehat {BHO} = {180^0}\) (hai góc kề bù) nên \(\widehat {AHO} = \widehat {BHO} \)\(= 180^0:2={90^0}\)

Tức là \(OM \bot AB\)

b)

 

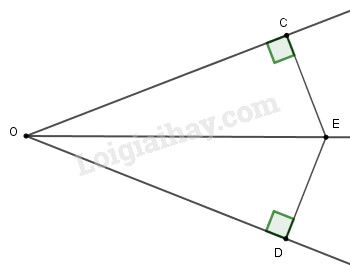
Xét hai tam giác vuông \(COE\) và \(DOE\) có:

+) Cạnh huyền \(OE\) chung

+) \(OC = OD\) (giả thiết)

Nên \(\Delta COE = \Delta DOE\) (cạnh huyền - cạnh góc vuông)

Suy ra \(\widehat {EOC} = \widehat {EOD}\) hay \(OE\) là tia phân giác của góc \(O.\)

Bài 5.4

Cho tam giác cân \(ABC, AB = AC.\) Trên các cạnh \(AB, AC\) lần lượt lấy hai điểm \(P, Q\) sao cho \(AP = AQ. \) Hai đoạn thẳng \(CP, BQ\) cắt nhau tại \(O.\) Chứng minh rằng:

a) Tam giác \(OBC\) là tam giác cân.

b) Điểm \(O\) cách đều hai cạnh \(AB, AC.\)

c) \(AO\) đi qua trung điểm của đoạn thẳng \(BC\) và vuông góc với nó.

Phương pháp giải:

a) Chứng minh tam giác \(OBC \) có hai góc \(OBC\) và \(OCB\) bằng nhau

b) c) Sử dụng: 

+) Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó

+) Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

Lời giải chi tiết:

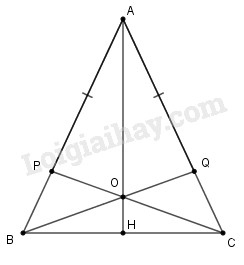
a) Xét \(∆ABQ\) và \(∆ACP\) có:

+) \(AP=AQ\) (gt)

+) \(\widehat A\) chung

+) \(AB=AC\) (gt)

Suy ra \(∆ABQ = ∆ACP\) (c.g.c) nên \(\widehat {ACP} = \widehat {ABQ}\).

Mặt khác \(\widehat {ACB} = \widehat {ABC}\) do tam giác \(ABC\) cân tại \(A\) (vì \(AB=AC)\) nên \(\widehat {OCB} = \widehat {OBC}\).

Suy ra tam giác \(OBC\) cân tại \(O.\)

b) Vì tam giác \(OBC\) cân tại \(O\) nên \(OB=OC\)

Xét hai tam giác \(AOB\) và \(AOC\) có:

+) Cạnh \(AO\) chung

+) \(AB = AC \) (giả thiết)

+) \(OB = OC\) (chứng minh trên)

Vậy  \(∆AOB = ∆AOC\) (c.c.c).

Suy ra \(\widehat {OAB} = \widehat {OAC}\) hay \(AO\) là tia phân giác của góc \(BAC.\)

Suy ra \( O\) cách đều hai cạnh \(AB, AC\) (tính chất).

c) Gọi giao điểm \(AO\) với \(BC\) là \(H.\)

Xét hai tam giác \(AHB\) và \(AHC\) có:

+) Cạnh \(AH\) chung 

+) \(\widehat {BAH} = \widehat {CAH}\) (theo câu b) 

+) \(AB = AC\)

Vậy  \(∆AHB = ∆AHC\) (c.g.c).

Suy ra \(HB = HC\) và \(\widehat {AHB} = \widehat {AHC} \)

Mà \(\widehat {AHB} + \widehat {AHC} = {180^0}\) (hai góc kề bù) nên \(\widehat {AHB} = \widehat {AHC} \)\(= 180^0:2={90^0}\)

Tức là \(AH \bot BC\)

Vậy \(AO \bot BC\) và \(AO\) đi qua trung điểm H của \(BC.\)

Bài 5.5

Cho hai đường thẳng song song \(a, b\) và một cát tuyến \(c.\) Hai tia phân giác của một cặp góc trong cùng phía cắt nhau tại \(I.\) Chứng minh rằng \(I\) cách đều ba đường thẳng \(a, b, c.\)

Phương pháp giải:

Sử dụng: 

+) Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó

+) Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

Lời giải chi tiết:

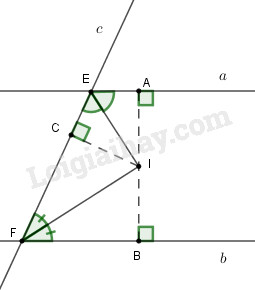
Gọi \(A, B, C\) lần lượt là chân đường vuông góc kẻ từ \(I\) đến \(a, b, c.\)

Xét hai góc trong cùng phía \(E\) và \(F.\)

Do \(I\) thuộc tia phân giác của góc \(E\) nên \(IA = IC.\)        (1)

Do \(I\) thuộc tia phân giác của góc \(F\) nên \(IC = IB. \)       (2)

Từ (1) và (2) suy ra \(IA = IB = IC,\) tức là \(I\) cách đều ba đường thẳng \(a, b, c.\)