Giải bài 5 trang 92 vở thực hành Toán 9
Cho tam giác ABC vuông tại A, có (widehat B = alpha ) (H.4.44).
Đề bài
Cho tam giác ABC vuông tại A, có \(\widehat B = \alpha \) (H.4.44).
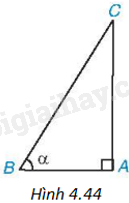
a) Hãy viết các tỉ số lượng giác \(\sin \alpha ,\cos \alpha \).
b) Sử dụng định lí Pythagore, chứng minh rằng \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
Phương pháp giải - Xem chi tiết
a) Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì:
+ Tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
b) + Theo ĐL Pythagore ta có \(A{C^2} + A{B^2} = B{C^2}\).
+ \({\sin ^2}\alpha + {\cos ^2}\alpha = \frac{{A{C^2}}}{{B{C^2}}} + \frac{{A{B^2}}}{{B{C^2}}} \)
\(= \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1\)
Lời giải chi tiết
a) Trong tam giác ABC vuông tại A, ta có: \(\sin \alpha = \frac{{AC}}{{BC}},\cos \alpha = \frac{{AB}}{{BC}}\).
b) Theo a), ta có
\({\sin ^2}\alpha + {\cos ^2}\alpha = \frac{{A{C^2}}}{{B{C^2}}} + \frac{{A{B^2}}}{{B{C^2}}} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}}\)
Theo ĐL Pythagore ta có
\(A{C^2} + A{B^2} = B{C^2}\)
nên \({\sin ^2}\alpha + {\cos ^2}\alpha = \frac{{B{C^2}}}{{B{C^2}}} = 1\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 5 trang 92 vở thực hành Toán 9 timdapan.com"







